20
--
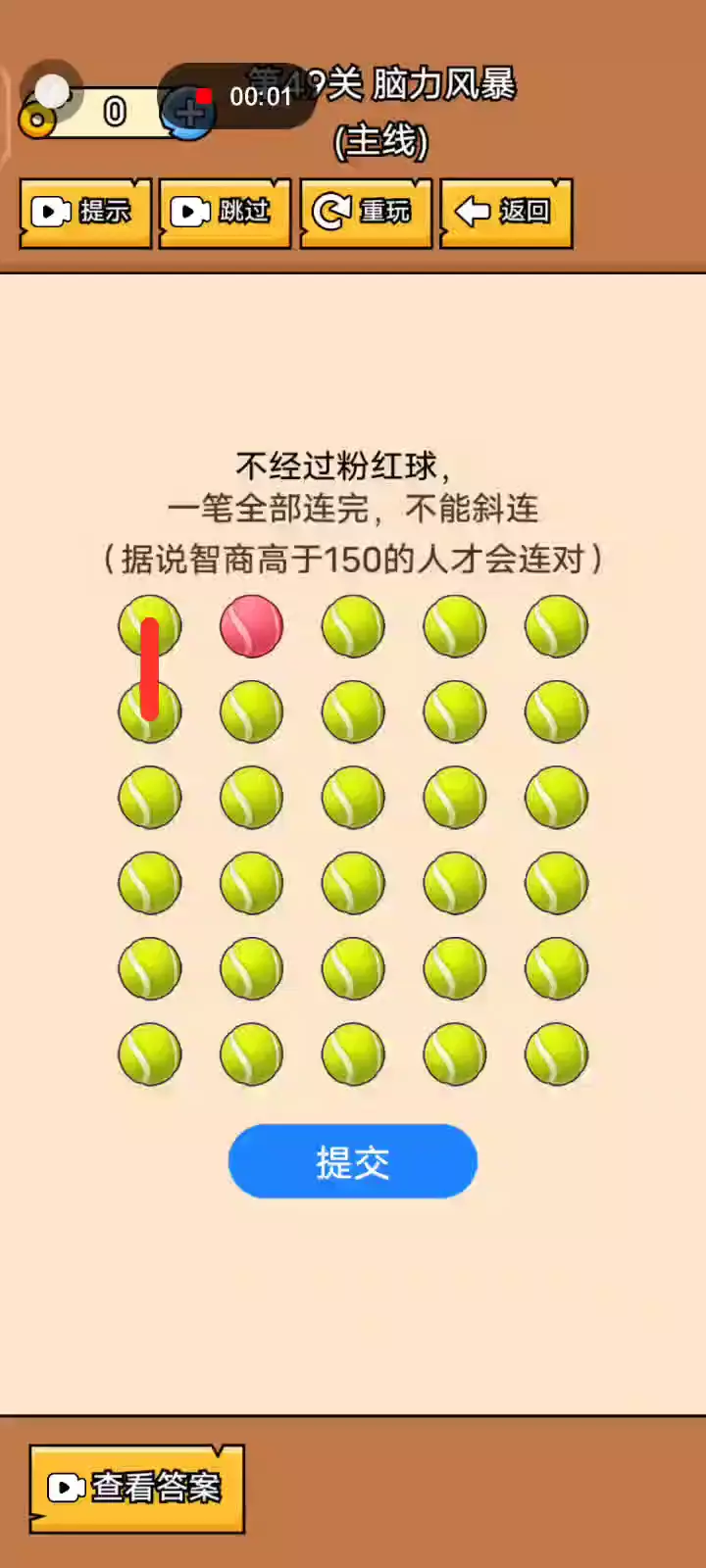
应该是不增反减
0 点赞
我要当校长(破解版)
难度:\begin{cases}
\frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\cdot\nabla)\boldsymbol{u}=-\frac{1}{\rho}\nabla p + \nu\Delta\boldsymbol{u}+\boldsymbol{f}\\
\nabla\cdot\boldsymbol{u}=0
\end{cases}
各符号含义:\boldsymbol{u}(x,t) 是流体速度矢量场,p(x,t) 是压强场,\rho 是流体密度,\nu 是运动黏性系数,\boldsymbol{f}(x,t) 是作用于流体的外力场,\Delta 是拉普拉斯算子,\nabla 是梯度算子,\nabla\cdot\boldsymbol{u}=0 对应不可压缩流体的质量守恒条件。
星数:1,原因:纯马扁人
展开






 我要当校长(破解版)
我要当校长(破解版)