ć°ĺŚ
这是我原始WORD文档的重新制作。我真心希望内容能被理解,因为Steam的格式选项确实不太适合包含大量希腊字母、下标和上标的数学内容。 如果下载WORD文档,请以网页格式查看,因为部分图片无法完整显示在A4页面上。 祝好 MAD 基础机动 基础机动
单一推进在6个方向之一产生的效果 •每个轨道都处于通过其绕行物体质心的平面上。 •大多数轨道是椭圆,绕行物体位于两个焦点之一。 •新轨道和旧轨道必须在执行机动的点处相切。
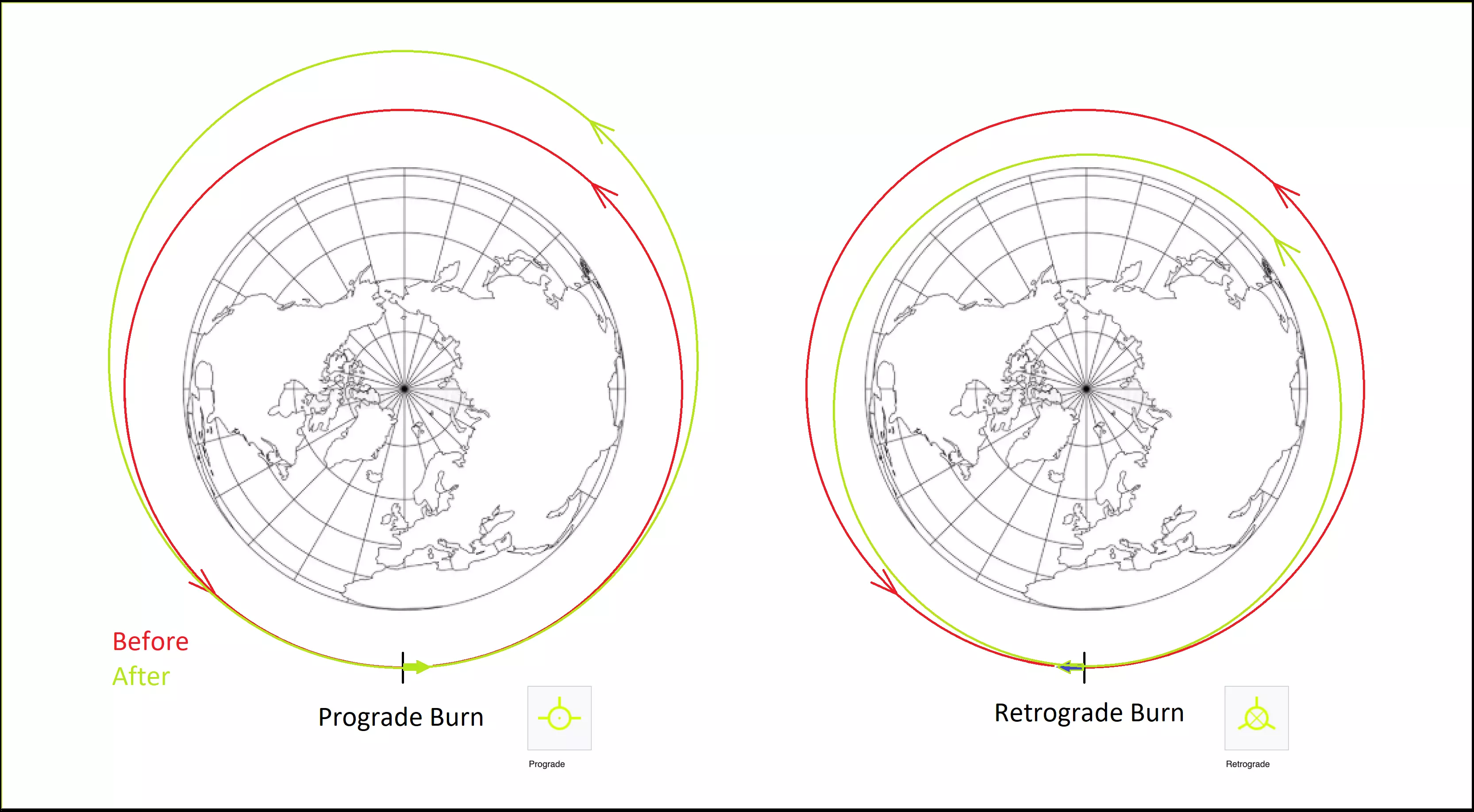
顺行方向——轨道运行的方向。顺行点火可增加轨道速度,从而增加半长轴。 逆行方向——与轨道运行相反的方向。逆行点火可降低轨道速度,从而减少半长轴。 顺行/逆行点火用于轨道转移和准备再入大气层,几乎适用于所有情况。
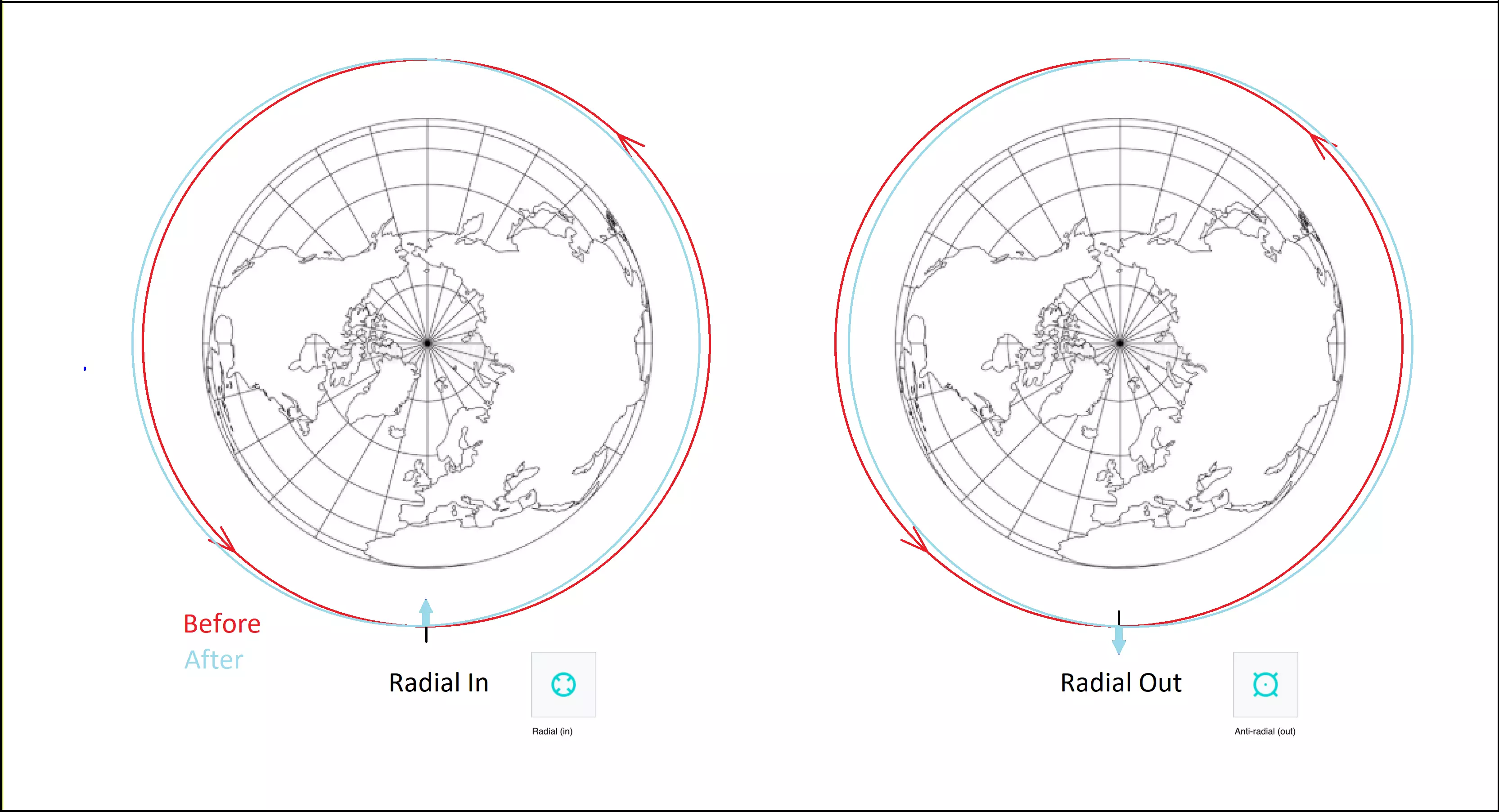
径向燃烧有利于轨道交会,但不太适合向行星投掷炸弹。如果想向行星投掷炸弹,最好选择反向发射。
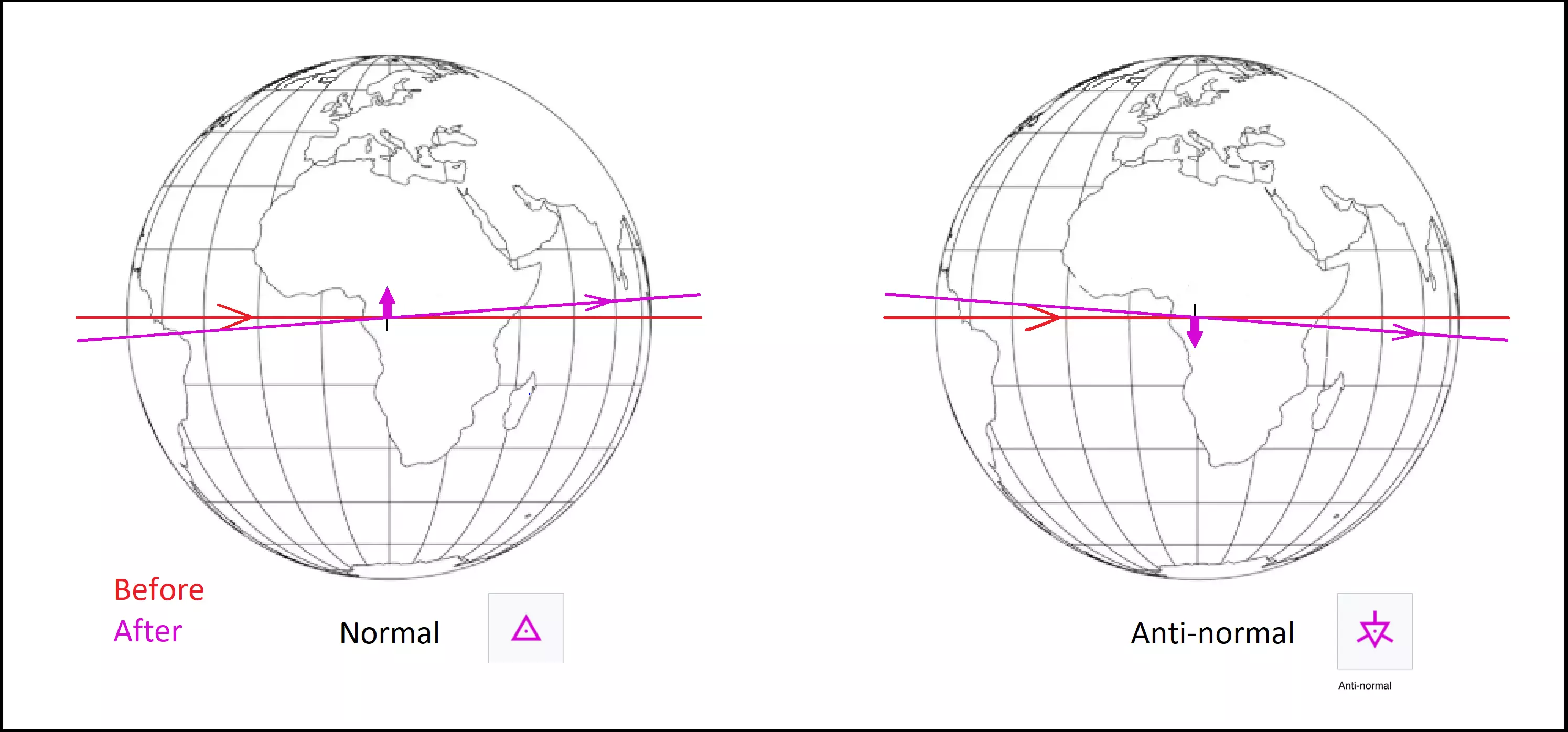
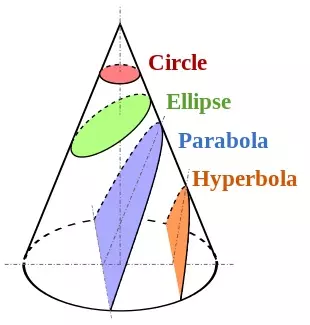
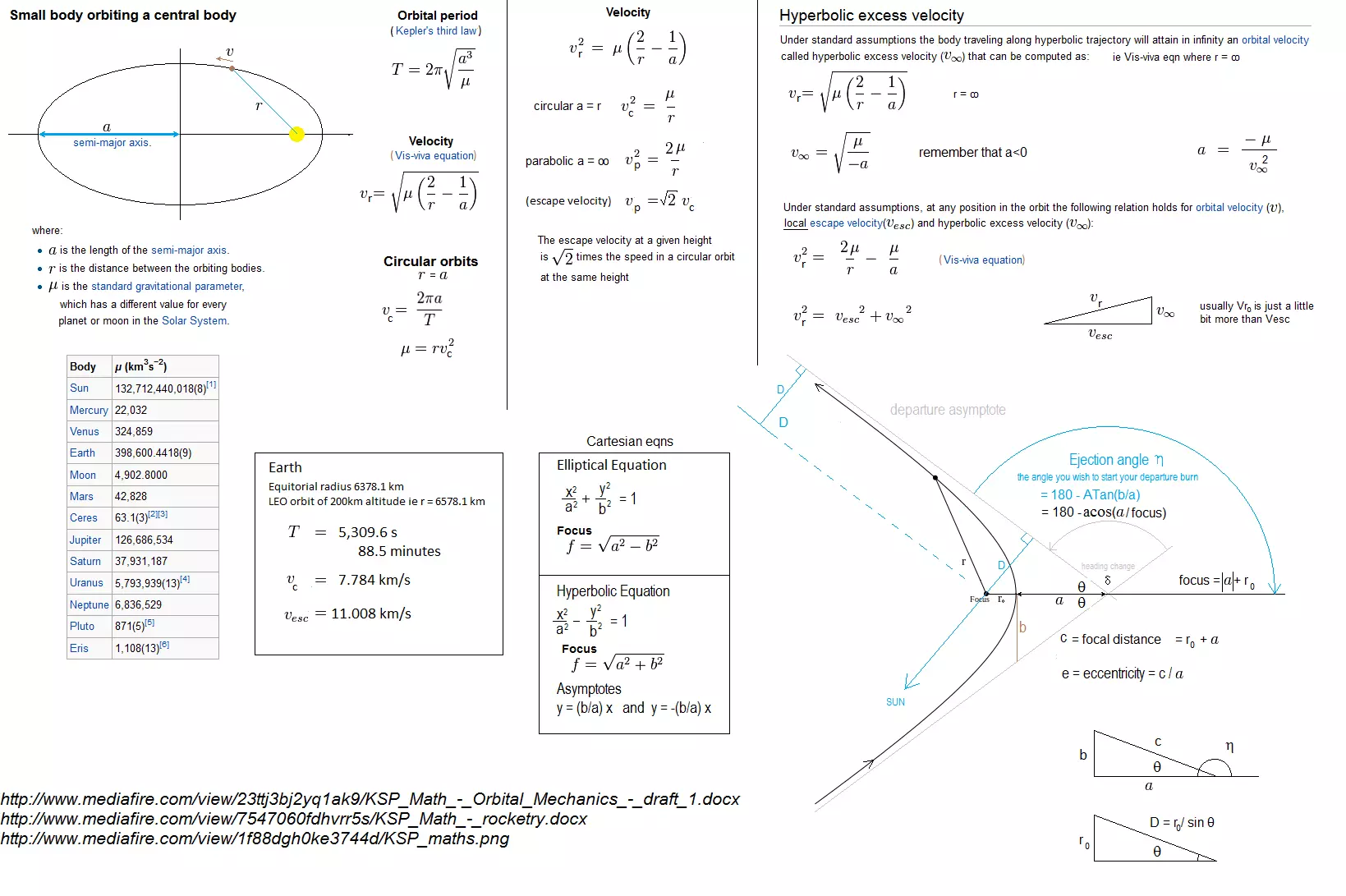
轨道倾角的改变对于调整轨道平面或将卫星送入倾斜轨道至关重要。 如果要匹配另一个轨道平面,必须在两个轨道平面的相交点,即升交点或降交点处执行机动。 在轨道速度较低的更高海拔处执行机动,能更节省燃料。 轨道力学、作用范围与圆锥曲线 轨道力学 计算物体在多个引力体作用下的空间运动是非常困难的,有人甚至认为这是不可能的,这还没有考虑广义相对论效应。 因此,我们将多体问题简化为多个二体问题,具体来说,就是你和你的航天器绕着一个质量大得多的天体运行,例如卫星、行星或恒星。引力范围 每个大质量天体都会在其周围的局部空间形成引力主导区域,通常称为【引力范围】(SOI)。 引力范围的边界是两个天体(例如一颗行星和另一颗更大的天体恒星)之间的引力达到平衡的位置。在引力范围内,行星的引力占主导地位;而在引力范围外,恒星的引力则占主导地位。因此,卫星的引力范围位于行星的引力范围内,而行星的引力范围又位于恒星的引力范围内。 重要的一点是,当处于某个天体的引力范围内时,我们可以忽略宇宙中除该主天体和你的飞船之外所有其他天体的引力影响。在《坎巴拉太空计划》中,每个恒星、行星和卫星的【 sphere of influence (SOI)】都可以在游戏维基上查询到。 圆锥曲线 正如上文所述,我们将多体问题简化为多个二体问题;这也是《坎巴拉太空计划》所采用的方式。 在每个【 sphere of influence (SOI)】内,我们将围绕主天体进行轨道运行,通常是椭圆轨道;但根据速度的不同,也可能是其他圆锥曲线轨迹,如圆形、椭圆、抛物线和双曲线。 它们被称为圆锥曲线的原因是,这些轨迹代表了通过圆锥体的不同几何截面。
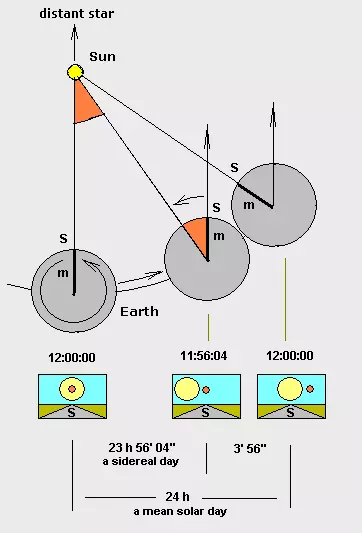
现在来澄清好莱坞最大的神话之一:太空中的物体不会落回地球,它会绕地球运行,并且会继续绕地球运行;在忽略太阳风、大气阻力等因素且没有动力的情况下,会永远运行下去。月球绕地球运行至今已有几十亿年。因此,如果绕地球轨道运行的“企业号星舰”突然失去动力,它不会直接坠向地面。
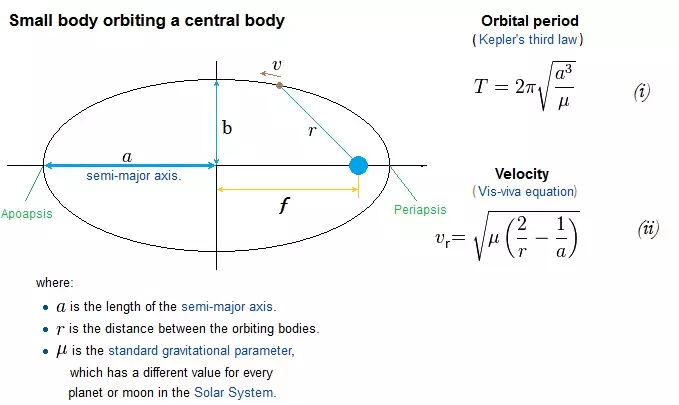
在围绕坎星的椭圆轨道中,坎星(以蓝色圆圈表示)是椭圆的焦点之一。当我们远离坎星时,速度会降低,因为动能会转化为势能。 - 远坎点是轨道上距离坎星最远的点,此处速度最低。 - 近坎点是轨道上距离坎星最近的点,此处速度最高。 远坎点和近坎点位于彼此正对面,它们之间的距离为长轴,长轴的一半称为半长轴【a】——请记住这一点,因为你会经常用到它。 (椭圆还有半短轴【b】,其中对于椭圆而言)
轨道周期T,即完成一次完整公转所需的时间,由开普勒行星运动第三定律给出。
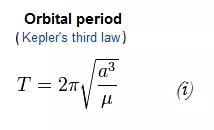
我们在椭圆轨道任意位置的速度均可通过活力公式计算得出。
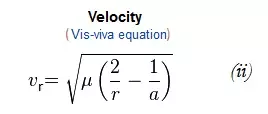
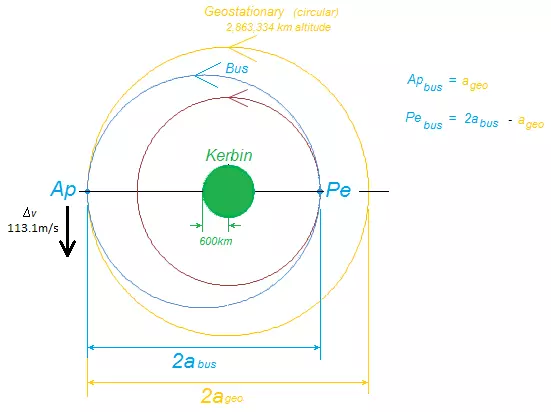
通过这两个方程,你可以在太阳系或坎巴拉系统中的任何位置绘制粗略轨道,但这部分内容我们稍后再详细讨论。 对于大多数轨道机动,我们只需要关注在远地点或近地点的速度,以及需要如何调整这个速度来获得我们想要的轨道。人们在谈论太空旅行时提到的Δν,指的就是这种速度的改变量。 Δν只是表示速度变化的数学术语。希腊字母Δ(德尔塔)在数学符号中用于表示某事物的变化,这里它代表速度ν的变化,因为我们为了省事,不想每次都写“速度变化量”。 到目前为止,我一直在谈论速度,而不是 velocity(速度矢量);velocity 指的是在特定方向上的速度,也就是矢量。示例1 - 将卫星从80千米高度的低坎星轨道转移至地球静止轨道需要多少Δν( delta-v,德尔塔-v) 将卫星从80千米高度的低坎星轨道(绿色)转移至地球静止轨道(红色)需要多少Δν( delta-v,德尔塔-v)。 图1
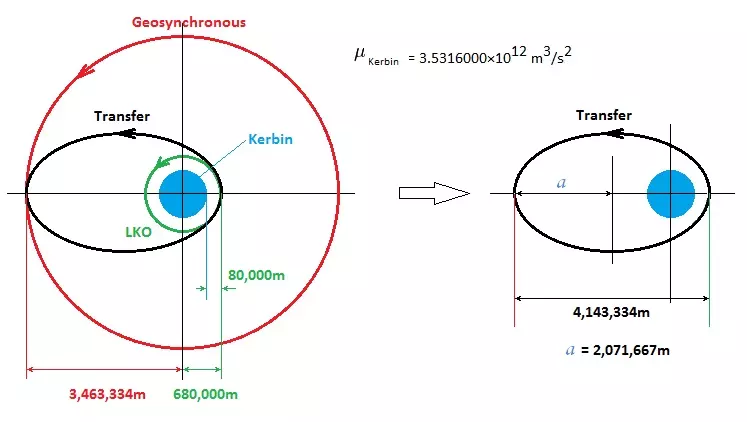
低轨道(LKO)高度80千米相当于680千米(680,000米)的轨道半径,因为Kerbin的赤道半径仅为600,000米。 (此信息来源于坎巴拉太空计划维基) (作为对比,地球的赤道半径为6,371千米) 需要说明的是,Kerbin的大气层在70千米高度处结束(同样来自坎巴拉太空计划维基),因此低轨道高度设定为80千米。 地球同步轨道是一种周期恰好为1个恒星日的圆形轨道,恒星日是行星相对于恒星完成360度自转所需的时间。 不要将其与太阳日混淆,太阳日是太阳出现在天空中同一位置所需的时间。两者的差异是因为行星同时也在围绕恒星运行。大多数人所说的“天”指的是太阳日,即一年约有365.25个太阳日。 如果抬头观察地球同步轨道上的物体,它看起来会一直处于天空中的同一位置。我们将通信卫星送入地球同步轨道,就是因为它们看起来位置固定,这样我们就可以将卫星天线对准它们,而无需使用复杂的跟踪机制。 根据《坎巴拉太空计划》维基,1个恒星日为21549.425183秒。 根据开普勒第三定律,对于圆形轨道,轨道半径r等于半长轴a,即圆的半径也是其半长轴。因此,已知所需的轨道周期T,就可以求解半长轴a。
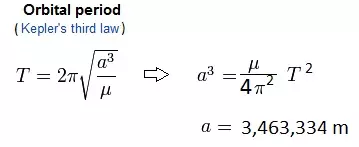
我失去你的注意力了吗?你可能会问这个“u”是什么东西? “µ”是“标准重力参数”,它不是“u”,而是一个有趣的希腊字母“mu”(μ)。 我敢说数学家和物理学家们就是把这些希腊字母都扔进来迷惑人的。 不管怎样,天体的“μ”是引力常数G和天体质量M的乘积,它在太阳系/坎巴拉系统中每个天体都是独一无二的。 不要把坎巴拉的μ和太阳(恒星)的μ弄混了,并且要确保你使用的单位是正确的。 我会尽量使用国际单位制,用米和秒。 另外,在处理这么大的数字时,不要太纠结于小数位数。参考图1,已知起始轨道和结束轨道的半径,我们可以计算出椭圆的半长轴a。ae是椭圆半长轴的缩写。
现在我们可以使用活力公式来计算圆形轨道和椭圆轨道在远地点和近地点的速度。
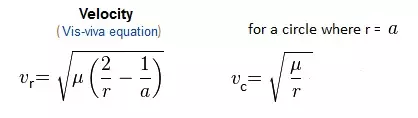
近地点 r = 680,000米 a = 2,071,667米 ve = 2,946.6米/秒 vc = 2,278.9米/秒 Δν1 = ve – vc = 667.7米/秒 (即椭圆轨道速度 - 圆形轨道速度) 也就是说,我们需要沿顺行方向加速667.7米/秒,从圆形轨道转变为椭圆轨道,以到达地球静止轨道。 远地点 r = 3,463,334米 a = 2,071,667米 ve = 578.5米/秒 vc = 1009.8米/秒 Δν2 = vc - ve = 431.3米/秒 也就是说,我们需要沿顺行方向加速431.3米/秒,从椭圆转移轨道转变为地球静止轨道的圆形轨道。 总Δν = Δν1 + Δν2 = 1,098.9米/秒 需要注意的是,如果你从地球静止轨道返回80公里近地轨道且不进行大气制动,那么Δν值将完全相同,只是此时需要沿逆行方向点火。太阳日=21600秒 太阳年=9203544.6秒 恒星日=太阳日×太阳年÷(太阳年+太阳日) 补充说明:恒星日 太阳日是太阳出现在天空中同一位置所需的时间。 恒星日是恒星出现在天空中同一位置所需的时间。 两者存在细微差异,这是因为地球(行星)会围绕太阳公转。
通常我们会用精确的时钟来测量这段时间,但如果你愿意,也可以通过一个量来计算另一个量。 在《坎巴拉太空计划》中: 1个太阳日=6小时(21600秒) 1个太阳年=9203544.6秒(426.09天) 在1个太阳日里,行星会绕恒星运行:216000/9203544.6×360=0.84度,因此恒星日会缩短0.84度。也就是说,1个恒星日是太阳日的(360-0.84)/360。 你也可以从时间角度来理解:0.84/360×216000秒=50.693512秒,因此恒星日比太阳日短50.693512秒。 在《坎巴拉太空计划》中,1个恒星日的时长为21549.425183秒。 补充说明:太阳日是指太阳连续两次出现在天空同一位置所需的时间(前提是你自身的经度没有发生变化)。如果你移动了位置,太阳再次出现在同一位置所需的时间会因移动距离而有所不同。 如果你有精确的时钟,可以测量太阳在天空中同一位置出现所需的时间,并利用该时间计算你与原始位置的经度变化。 18世纪的航海家曾使用这种方法在海上计算船只的位置。 六分仪是一种用于精确测量角度的仪器,通常用于测量太阳(或星星)与地平线的夹角。 1节是速度单位,等于每小时1海里。 船只沿子午线以1节的速度航行时,每小时大约会移动1角分(即1/60度)的地理纬度。【每度经度对应60海里】旁注 - 将多颗卫星送入地球静止轨道 如果想要将卫星送入地球静止轨道,你可能需要放置多颗卫星,以便能够与全球任何地点进行通信。
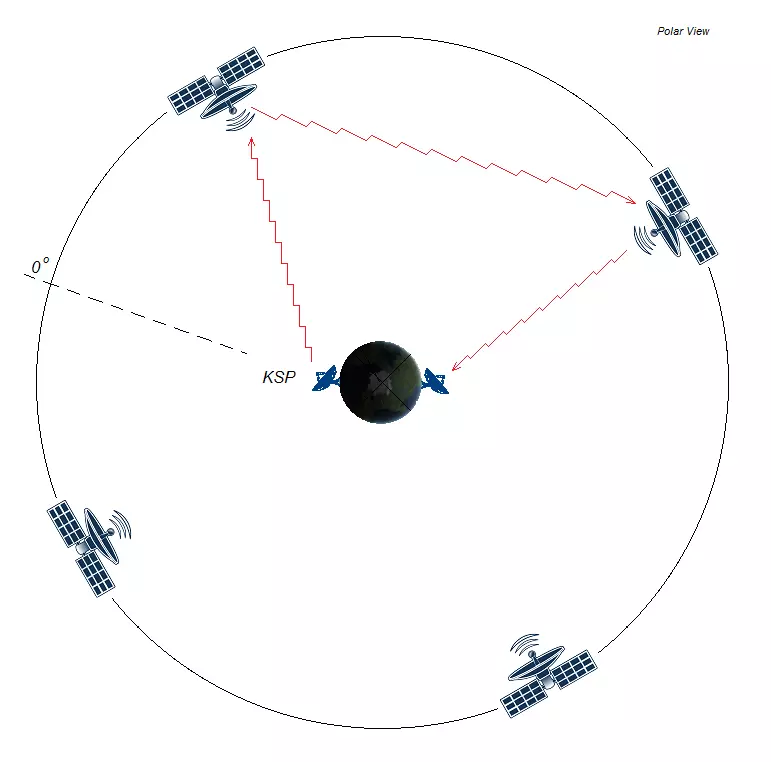
问题:如何确保卫星在轨道上均匀分布?例如3颗卫星彼此间隔正好120度,4颗卫星彼此间隔正好90度。 答案:让母船释放它们。8-) 问:如何把大象放进冰箱? 答:打开冰箱门,把大象放进去,关上冰箱门。很简单8-) 问:如何把长颈鹿放进冰箱? 如果你想说“打开冰箱门,把长颈鹿放进去?”那就太傻了。 答:打开冰箱门,把大象拿出来,然后把长颈鹿放进冰箱,关上冰箱门。9-) 答案:让母船释放它们。对于3颗卫星的网络,母船的周期是地球同步周期的2/3。对于一个4颗卫星的网络,母航天器的周期为地球同步周期的3/4。(注:还有其他可行的解决方案,但我尝试让事情保持简单)这样,母航天器的每个轨道相当于地球同步轨道上的120度/90度。地球同步周期等于一个恒星日,即21549.425秒。由于斯科特的视频介绍了3颗卫星的网络,我将介绍4颗卫星的网络。我们需要求出母航天器椭圆轨道的半长轴“a”。
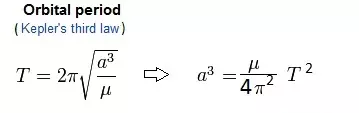
T = 四分之三恒星日 = 四分之三 × 21,549.425183秒 = 16,162.069秒 标准引力参数,ukerbin = 3.5316000×10^12 立方米/平方秒 求解半长轴 a = 2,858,919.28米
3/4恒星日的轨道特性 远地点高度=2863.33千米(即地球静止轨道) 近地点高度=1654.50千米 - 进入轨道 - 将近地点圆化至约1654.5千米 - 以 Mun 为参考,将轨道倾角设为0.0度(即赤道上空) (在轨道速度较低时改变倾角效率更高,但如果想在低 Kerbin 轨道改变倾角也可以) - 将轨道圆化至1654.5千米(速度=1251.6米/秒) - 规划一个远地点=2863千米的转移轨道33公里即地球静止轨道 如果你愿意,可以将近地点直接设置在坎巴拉太空中心上空,第二和第三颗卫星的经度将分别为±45度,这样坎巴拉太空中心就有两颗卫星可供选择(以防其中一颗发生故障) * 执行转移 * 每次到达远地点(地球静止轨道)时释放一颗卫星并将其轨道圆化 圆化轨道所需的Δv约为113.1米/秒 地球静止轨道的轨道速度为1009.8米/秒 尽量将轨道周期调整为16161.319秒(5小时59分8.425秒) 【Remote Tech】是一个处理逼真卫星通信的模组针对3颗卫星 地球同步轨道卫星的轨道特性(2/3恒星日) 远地点高度 = 2863.33千米(即地球静止轨道) 近地点高度 = 1222.70千米 示例2 - 转移需要多长时间? 我们已经计算出椭圆的半长轴“a”,只需将其代入开普勒第三定律即可得到轨道周期;转移时间为半个周期。
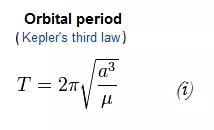
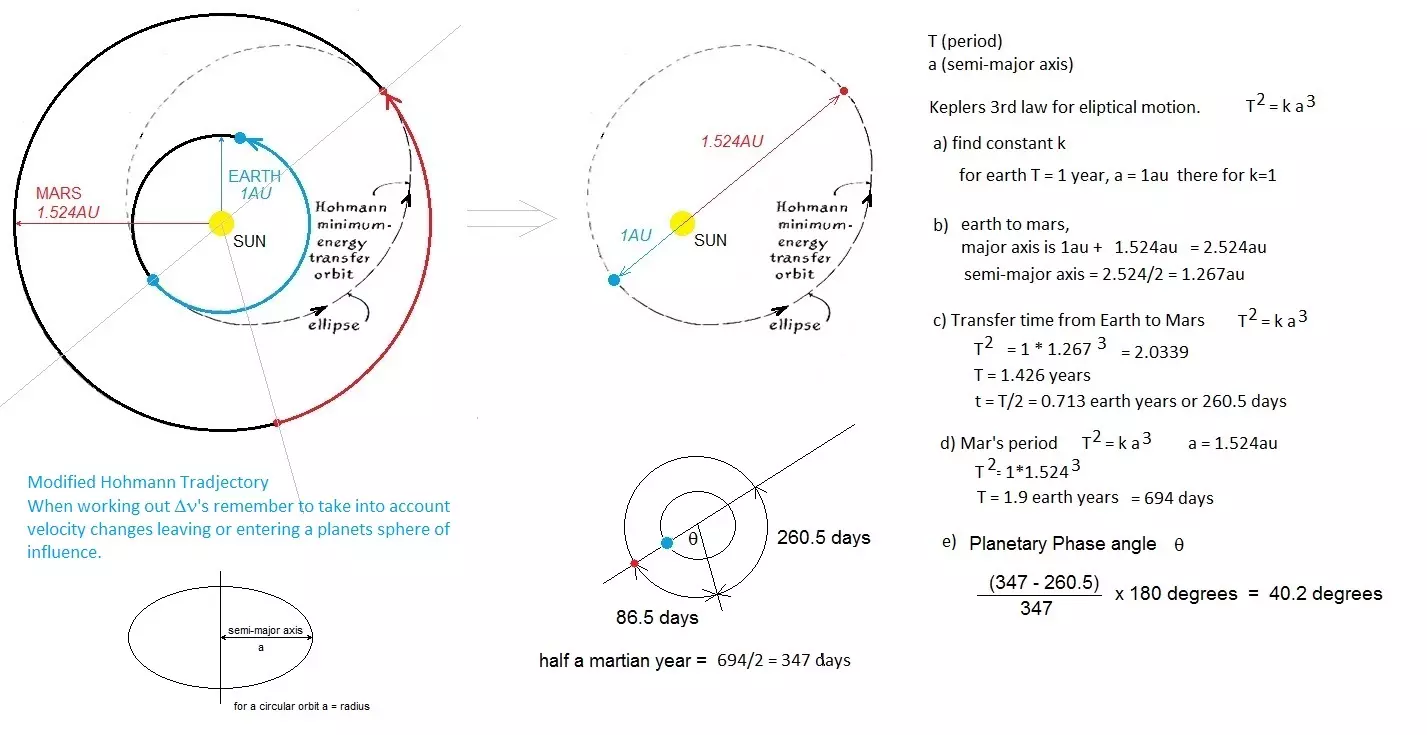
轨道周期T=9970秒 转移时间为其一半,即9970/2=4985秒→1小时23分5秒 这是一个物体仅通过两次短时间点火,沿椭圆轨道漂移完成机动所需的时间。 地球到火星
霍曼转移与双脉冲机动 这种机动被称为霍曼转移。它是太空中移动效率最高的方式之一,也是最容易计算和执行的方式,因为所有机动都在远地点或近地点进行。这是大多数《坎巴拉太空计划》玩家的做法。 在游戏中,你无需进行任何计算,只需将飞船朝向顺行或逆行方向,点火直到椭圆轨道扩展到目标位置,然后沿着椭圆轨道进行下一次点火。 在远地点或近地点改变轨道效率最高,但你也可以在其他位置进行……从低圆轨道到高圆轨道的霍曼转移
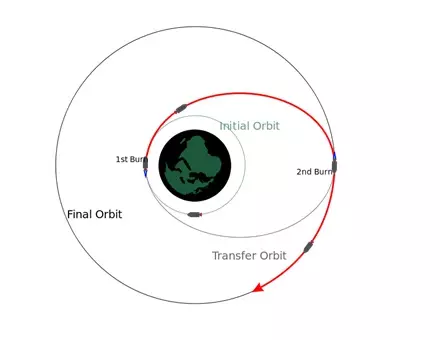
如果你准备消耗额外燃料,可以缩短旅行时间。通用双脉冲转移
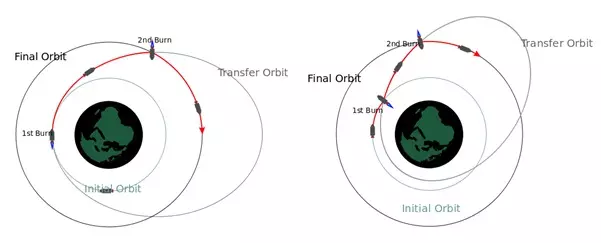
注意:我们所有的转移轨道都是椭圆的一部分。 如果你真的想计算,可以使用活力公式来计算椭圆任意部分的速度,然后利用几何恒等式x²/a² + y²/b² = 1来计算该点的分向量,并对转移椭圆执行相同操作等等。 通过这种方式计算你的Δν,但我现在肯定不会这么做。还有一种你需要了解的机动方式,即双椭圆转移。在某些情况下,它所需的Δv(德尔塔-v)比霍曼转移机动更少。计算起来很简单,因为它就是两个霍曼转移接连进行,但执行起来确实非常耗时。
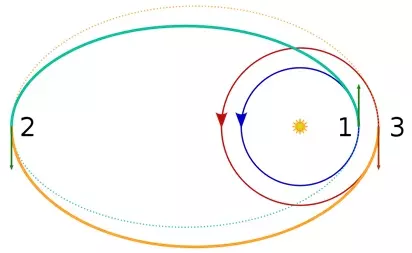
圆锥曲线补丁 在每个【球体影响范围】内,我们通常会沿着椭圆轨道围绕主天体运行;但根据速度不同,也可能是其他圆锥曲线轨迹,如圆形、椭圆、抛物线和双曲线。 如果我们想去【Kerbin】球体影响范围之外的地方,比如其他行星,该怎么办呢? 假设我们要前往【Duna】: 1.首先,必须沿着双曲线轨迹离开【Kerbin】的球体影响范围。 2.这会使我们进入【Kerbol】恒星的球体影响范围。如果计算正确,我们将沿着椭圆轨道飞行,最终与【Duna】的球体影响范围相交。 3.进入【Duna】的球体影响范围后,我们会沿着双曲线轨迹掠过【Duna】。如果计划在那里停留,就需要适当减速,以被【Duna】捕获并留在其球体影响范围内。我们已经进入了三个不同的球体引力影响范围(SOI),在每个球体引力影响范围内,我们实际上都在进行不同的圆锥曲线轨道飞行。我们的整个旅程本质上是由不同圆锥曲线段拼接而成的,也就是拼接圆锥曲线法。 这是一种近似方法,是对非常复杂的多体问题的一种非常好的近似。 我们的任务是确保在从一个球体引力影响范围过渡到另一个时,我们的速度和方向是正确的,这样才能到达我们想去的地方。 从Kerbin到Duna
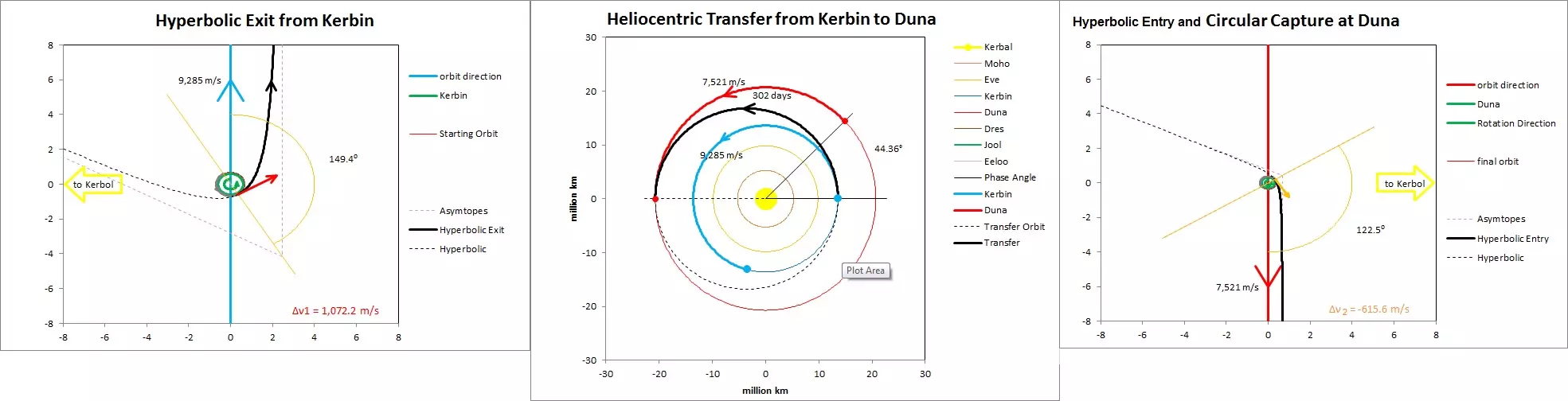
从计算角度出发,我们先以日心说(希腊语中意为“以太阳为中心”)的方式围绕恒星坎星(Kerbol)进行转移。我们知道,由于轨道速度远低于坎星的逃逸速度,我们将沿椭圆轨道运行。 就像霍曼转移一样,我们希望椭圆轨道的一端——这里是近星点(periapsis)——位于坎星轨道上,而椭圆轨道的远星点(Apopsis)则位于邓恩星(Duna)轨道上。 对于能量效率高的椭圆转移而言,当然,你也可以选择更快但燃料效率更低的双脉冲转移,但为了计算简便,我们将采用霍曼式转移。从技术上讲,这是一种日心转移,因为其一端或多端存在质量体,但当我说类似霍曼转移时,希望你能更好地理解。就像霍曼转移一样,我们可以计算近拱点和远拱点的椭圆速度。这些将是我们离开Kerbin的球体影响范围(SOI)或进入Duna的球体影响范围(SOI)时所需的速度。至于方向,我们将沿着Kerbin的顺行方向离开,即Kerbin绕恒星运行的方向。
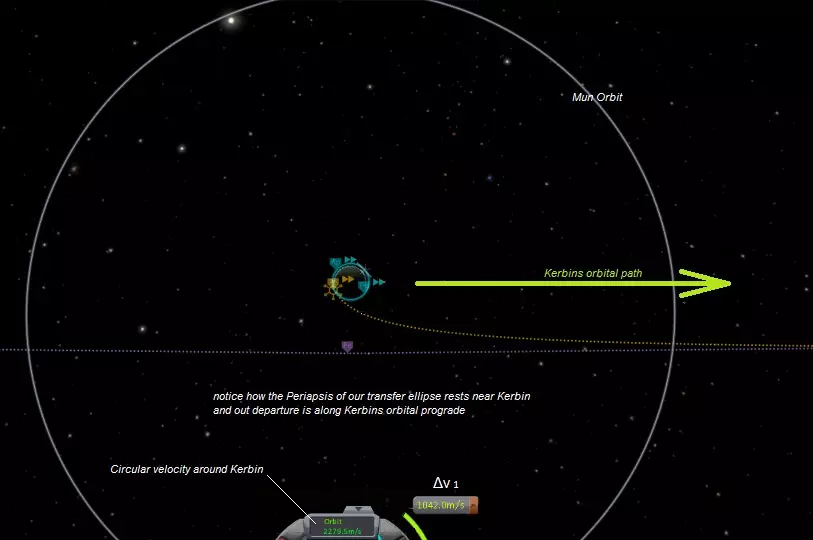
如果我们要前往内行星,我们会沿着坎星的逆行方向出发,因为我们正试图降低围绕恒星坎博的轨道速度。 了解离开坎星星球影响范围(SOI)所需的速度,能让我们计算出离开坎星所需的速度。这个速度通常被称为“逃逸速度”。 它是离开坎星的双曲线轨道在近拱点的速度。 我们的第一个Δν冲量将是逃逸速度与轨道速度之间的差值,在此之后,所有轨迹都将是无动力的,直到我们需要在另一端的 Dres( Dres)周围制动,这将是我们的第二个Δν冲量。现在这带来了几个选择:我们是沿着Kerbin的轨道平面飞行,并进行小幅修正以转换到Duna的轨道平面,还是以略微偏离我们轨道平面的某个奇怪角度发射,以便以弹道方式抵达Duna。
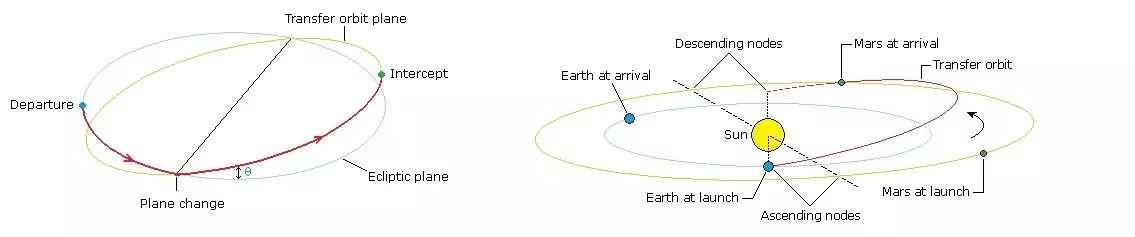
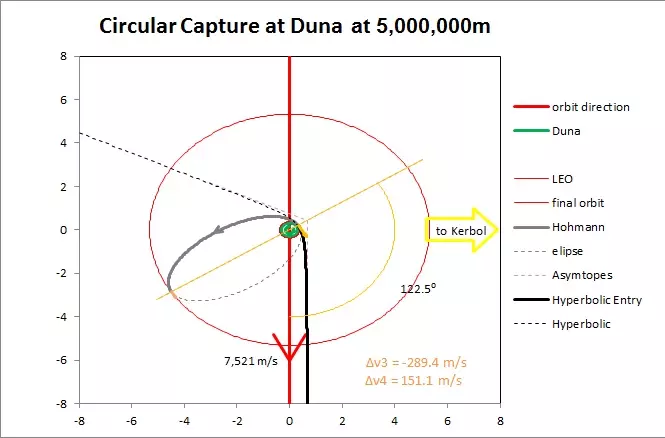
第一种方法需要在机动过程中进行轻微的轨道修正;第二种方法则需要在出发时进行轻微的矢量改变,这可能会导致两端额外消耗少量Δν(德尔塔-v)。 到达目标后,我们有以下几种选择: 1. 大幅减速,以特定半径进入围绕【Duna】的圆形捕获轨道。 2. 稍作减速,进入围绕【Duna】的椭圆捕获轨道。最大可能的椭圆轨道的远拱点刚好略低于【Duna】的引力范围,这被称为“边际捕获”。 3. 减速后进入椭圆轨道,然后在特定半径处圆化轨道。 4. 由于【Duna】拥有大气层,你可以进行大气制动,在【Duna】大气层中减速并着陆。或者进行一定程度的大气制动,进入围绕 Dres( Dres 是《坎巴拉太空计划》中的一颗行星,中文通常称为“ Dres ”或“ Dres 星”,此处按规则保留原词 )的轨道。大气制动可以帮你节省大量原本用于减速的燃料,从而减少甚至消除抵达目的地时的Δv( 速度增量 )需求。但要注意别意外烧毁了。一般来说,在离行星尽可能近的地方减速通常效率更高。进入 Dres 周围 5000 千米的圆形捕获轨道。
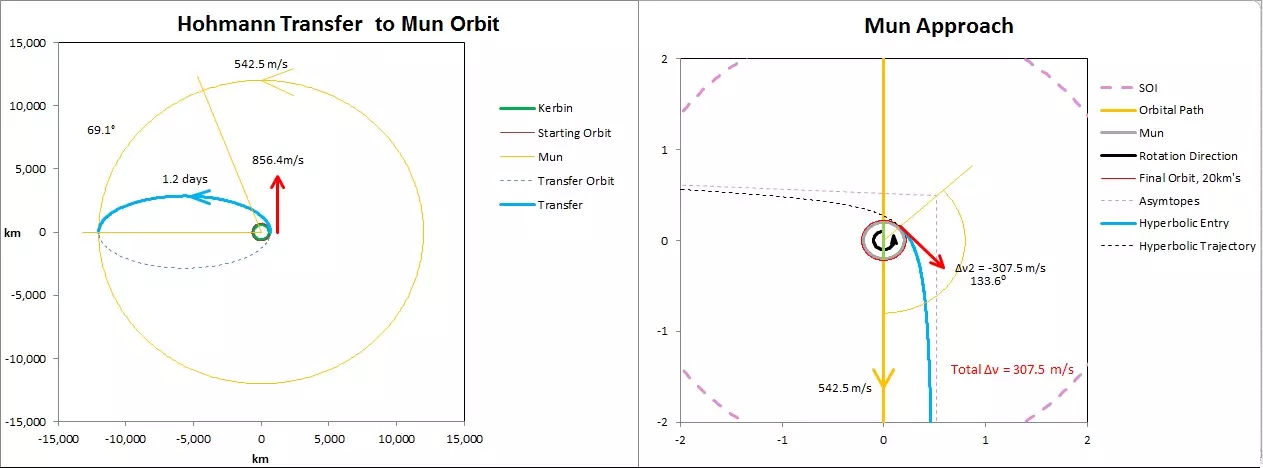
前往 Mun 前往 Mun 不需要我们离开 Kerbin 的 SOI(球体影响范围),但需要我们进入 Mun 的 SOI。记住,一旦进入某个天体的 SOI,所有计算都应视为二体问题,这里就是你和 Mun。 1) 抵达 Mun 很简单,只需规划一条椭圆轨道将我们送入 Mun 轨道。只需确保当你到达远地点时,Mun 正好在那里。 2) 一旦进入 Mun 的 SOI,你将沿双曲线轨道向 Mun 加速。如果你过于精准,导致轨道直接穿过 Mun 本身,不知道这算好运还是坏运。 再次说明,我们可以通过进入 Mun SOI 时的速度,计算出双曲线近地点的速度。我们的第一个Δν推进是将低地轨道(LKO)转变为能够抵达 Mun 轨道的椭圆轨道所需的推进,第二个Δν推进则是轨道减速,以便被 Mun 捕获。由于 Mun 没有大气层,大气制动是不可能的。不过实际上,我认为 Mun 有丰富的地貌,包括环形山、拱门,偶尔还有巨石或坠毁的飞碟。一次 Mun 之旅
双曲线轨道 圆形轨道:你的火箭以恒定速度运行,即圆周速度Vc。 椭圆轨道:你的火箭离行星越远速度越慢,最终会返回并进入环绕轨道。 抛物线轨道:你的火箭离行星越远速度越慢,但永远不会返回。其在无穷远处的速度为零。近地点的速度被称为“逃逸速度”。 双曲线轨道:你的火箭离行星越远速度越慢,但永远不会返回。其在无穷远处的速度大于零,这个速度被称为“双曲线剩余速度”ν∞。 当你进入或离开引力范围(SOI)时,你很可能正沿着双曲线轨道运行。
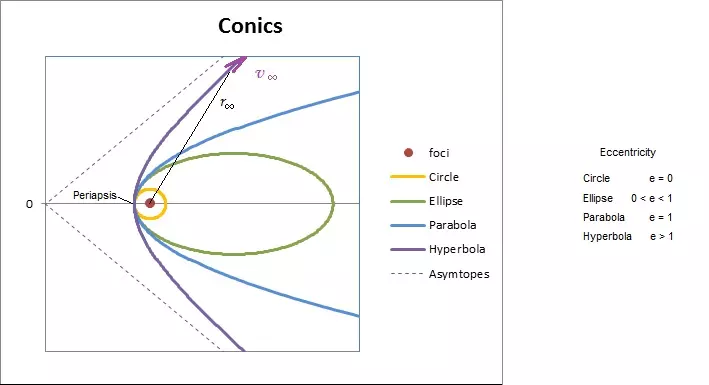
在近拱点(轨道上距离行星最近的点)的速度中,圆形轨道的速度最低。随着速度增加,轨道会逐渐变为椭圆,然后是抛物线,最终成为双曲线。任意给定半径r的速度可由活力公式得出。
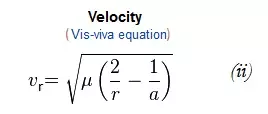
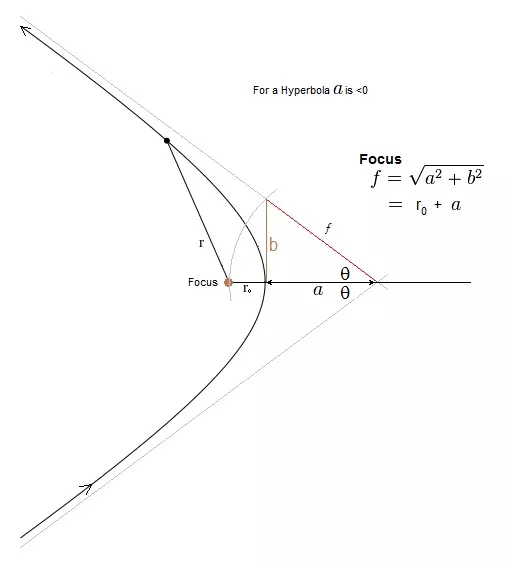
当r等于作用球半径(SOI)时,我们可以使用活力公式直接求解轨道半长轴a,一旦知道了a,就能计算出近拱点的速度,也就是我们的逃逸速度。
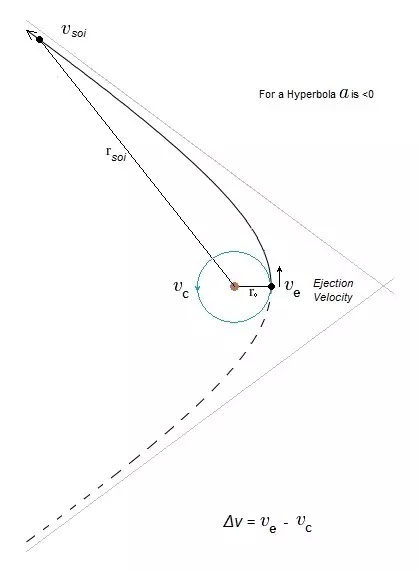
一旦你知道了你的逃逸速度,接下来只需确定将你送出 Kerbin 球体(SOI)并一路抵达 Duna 球体(SOI)所需的Δν冲量。 示例3 - 计算从 Kerbin 前往 Duna 的Δν 好的,让我们把所有内容整合起来,计算从 Kerbin 到 Duna 的Δν。 根据《坎巴拉太空计划》维基: Kerbin 轨道半长轴(aKerbin)= 13,599,840,256 米(圆形轨道) Duna 轨道半长轴(aDuna)= 20,726,155,264 米(略呈椭圆形)。为了获得更高的精度,你需要为计划使用的转移窗口计算 Duna 的精确轨道半径。
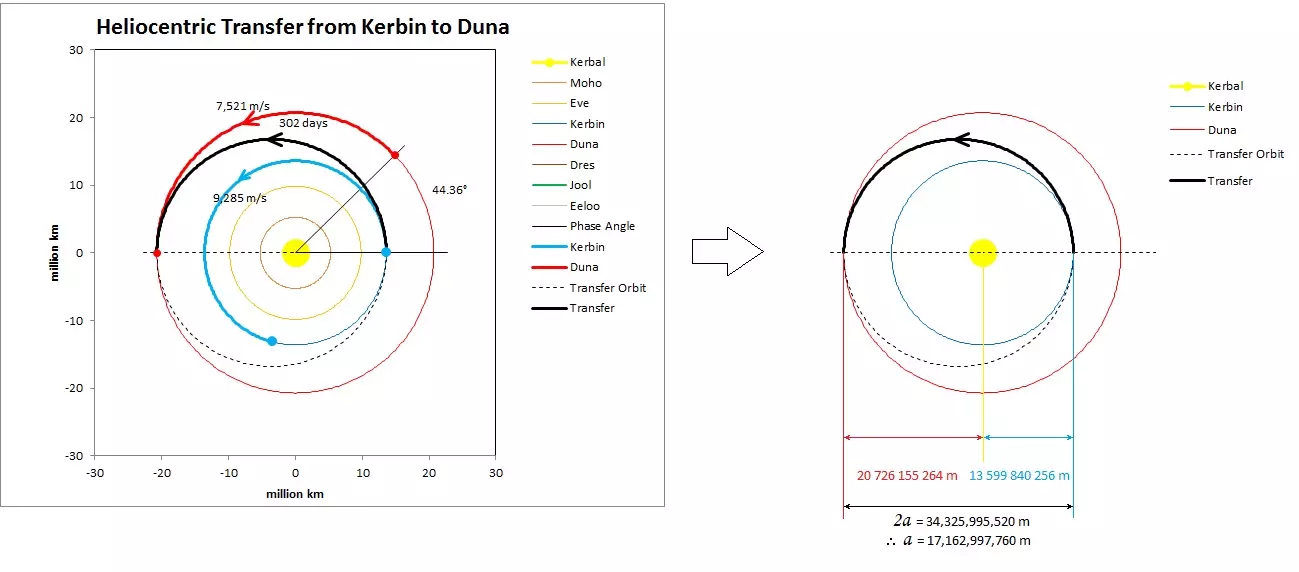
我们的转移椭圆半长轴 =(Kerbin轨道半长轴 + Duna轨道半长轴)/2 = 17,162,997,760 米 使用活力公式,我们可以计算出Kerbin和Duna的轨道速度,以及转移椭圆在远日点和近日点的速度 由于我们处于Kerbol的引力影响范围内,其引力参数µKerbol = 1.1723328×1018 立方米/平方秒
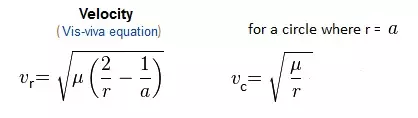
Kerbin轨道速度=√(1.1723328×10¹⁸/13,599,840,256)=9,284.50米/秒 Duna轨道速度=√(1.1723328×10¹⁸/20,726,155,264)=7,520.84米/秒 近拱点速度=√[1.1723328×10¹⁸×(2/13,599,840,256-1/17,162,997,760)]=10,202.85米/秒 远拱点速度=√[1.1723328×10¹⁸×(2/20,726,155,264-1/17,162,997,760)]=6,694.78米/秒 Kerbin作用范围:由于我们已在围绕Kerbol(恒星)的轨道上以9,284.50米/秒运行,而转移到Duna需要达到10,202.85米/秒,因此离开Kerbin作用范围所需的速度为(10,202.85-9,284.50)=918.35米/秒 Duna作用范围:同样,进入Duna作用范围的速度为(7,520.84-6,694.78)=826.05米/秒 离开Kerbin 当r=作用范围即84,159,286米时求a Kerbin引力参数=3.5316000×10¹²立方米/秒² 径向速度=918.35米/秒
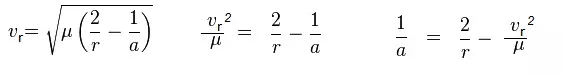
a = -4,650,267.67 米 没错,这是一个负数,所有双曲线轨道的半长轴都是负数。不用想太多,否则你会头疼的。这是数学上的设定。 我们假设从Kerbin的低轨道(LKO)出发,高度为80千米。 Kerbin的赤道半径为600千米,因此我们的出发轨道半径为680千米(680,000米)。 Kerbin的引力参数μ = 3.5316000×10^12 立方米/平方秒。 我们绕Kerbin的圆周轨道速度:vc = sqrt(μ/r) = sqrt(3.5316000×10^12 / 680,000) = 2,278.9 米/秒(这在《坎巴拉太空计划》中很容易验证)。 现在我们已知半长轴a,使用活力公式计算80千米高度处的逃逸速度。 Vr = sqrt(3.5316000×10^12 × (2/680,000 + 1/4,650,267.67)) = 3,338.64 米/秒。 由于我们已经以2,278米/秒的速度绕Kerbin运行。我们第一次推进的Δν为 Δν1 = vr – vc = 3338.64 - 2278.9 = 1059.71米/秒 经检查,计算结果为1055米/秒。 由于无法确定谁的计算更准确,也不清楚对方的假设条件或计算时保留的小数位数,但两者数值非常接近,考虑到μ值本身极大,因此差异几乎可以忽略不计。 到达 Dres 根据《坎巴拉太空计划》维基,Dres的大气层高度仅为50千米,因此我们选择在60千米高度进行Dres的圆轨道捕获。 Dres的赤道半径为320千米,因此轨道半径r = 380千米(380000米) μDres = 3.0136321×10¹¹ 立方米/平方秒 因此,vc = 根号(3.0136321×10¹¹ / 380000) = 8905米/秒 现在使用活力公式,我们可以计算双曲线参数a。已知当我们进入【Duna】的球体影响范围(47,921,949米)时,速度为826.05米/秒。 【Duna】的引力参数μ = 3.0136321×10¹¹立方米/秒²
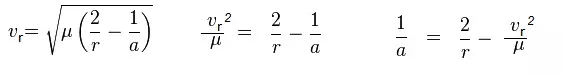
a = -449,942.67 近拱点r = 380,000米处的速度 Vr = 平方根(3.0136321×1011(2/380,000 + 1/449,942.67)) = 1,501.97米/秒 由于圆周速度为890.5米/秒,因此我们只需将速度改变1,501.97米/秒 - 890.5米/秒 = 611.4米/秒 即Δν2 = 611.4米/秒 olex计算结果为612.61米/秒;对于实际应用来说足够接近 从Kerbin前往Duna所需的总Δν为1,059.7米/秒 + 611.4米/秒 = 1,6711米/秒 加上轨道倾角变化所需的任何Δv(Delta-v,速度增量) 在“坎巴拉太空计划”中实现对“ Dres( Dres )”的边际捕获 相比进入“ Dres( Dres )”的圆形捕获轨道,进行边际椭圆捕获需要多少Δv(Delta-v,速度增量)? 这种椭圆的近拱点刚好在“ Dres( Dres )”大气层上方,远拱点刚好在“ Dres( Dres )”的希尔球(SOI, sphere of influence )下方;若远拱点更大,航天器将永远无法返回“ Dres( Dres )”。 根据“坎巴拉太空计划”维基,“ Dres( Dres )”的希尔球(SOI, sphere of influence )半径为47,921,949米,我们将远拱点设置为比该值短10公里,即47,911,949米。 我们的边际捕获椭圆参数: 近拱点 = 380,000米 远拱点 = 47,911,949米 椭圆半长轴a = (47,911,949 + 380,000)/2 = 24,150,974.5米 “ Dres( Dres )”的引力参数μ = 3.0136321×10^11 立方米/秒² 根据活力公式,近拱点的轨道速度 = sqrt(3.0136321×10^11 × (2/380,000 – 1/24,150,974.5)) = 1,254米/秒4米/秒 为了实现边缘捕获,我们需要将速度降低1501.97–1254.4=247.57米/秒,即Δν2=247.6米/秒 由于所有其他近拱点高度为60千米的椭圆捕获都处于这两个极端值之间,因此可以认为我们的Δν2介于这两个值之间 Δν2=247.6米/秒至615.6米/秒 此计算假设我们未进行大气制动 以下是从Kerbin前往Duna的部分游戏截图 从Kerbin出发

椭圆轨道转移至【Duna】
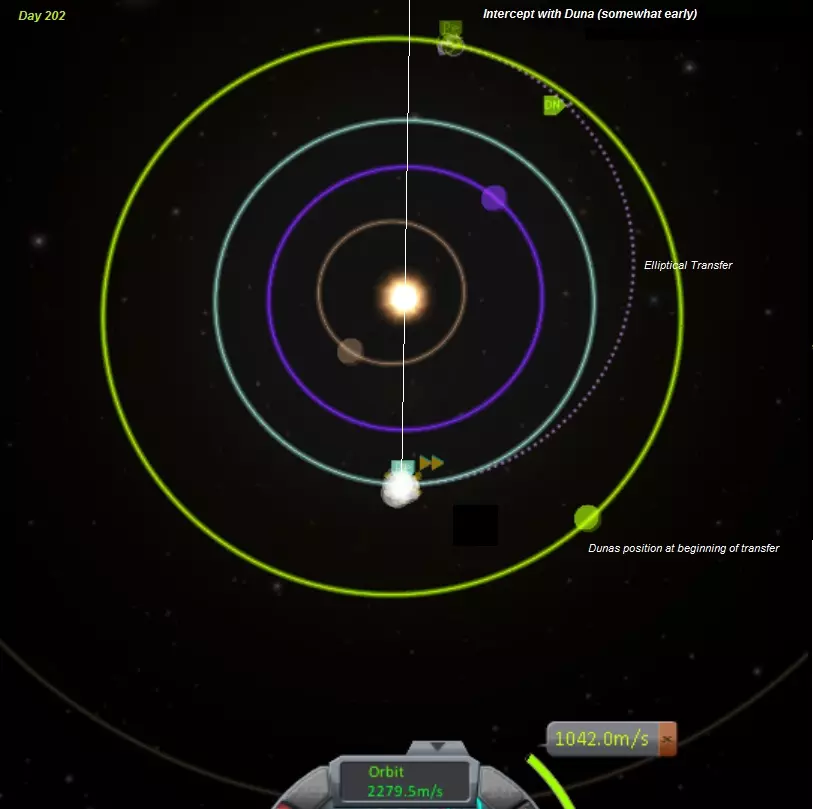
我们提前抵达了 Dres,哎呀,我早到了28天,最佳出发时间本应是第230天。就在 Dres 的作用范围外。
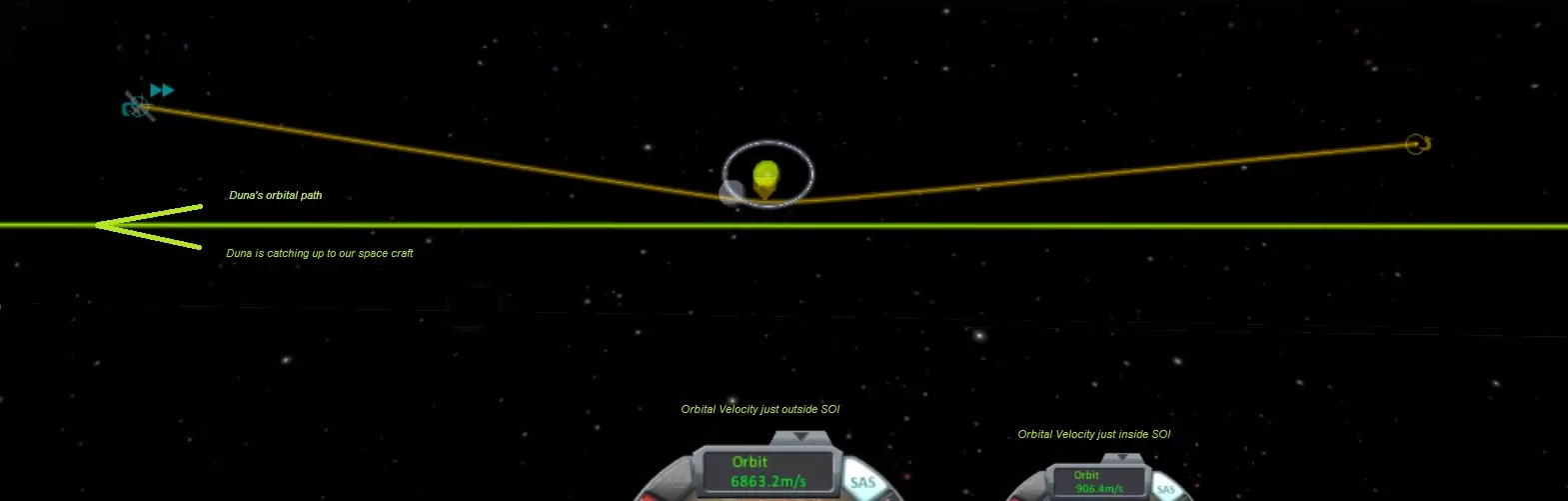
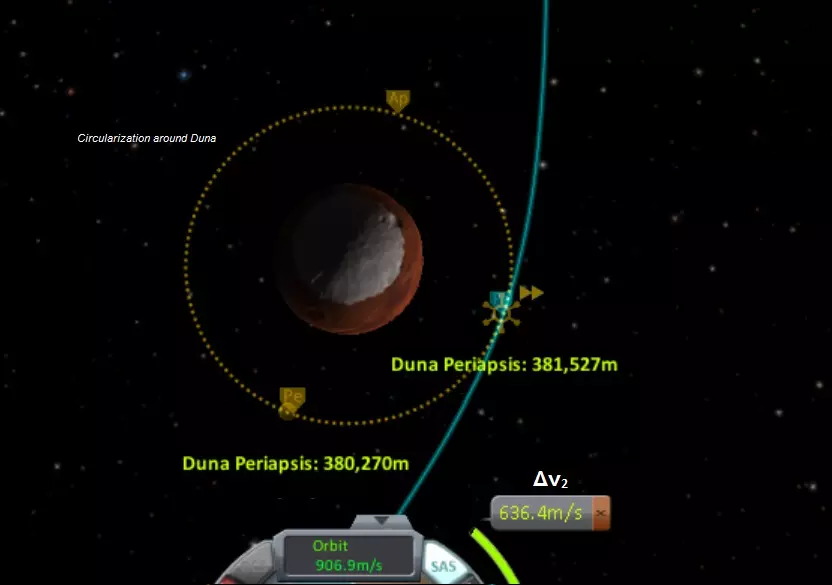
在 Dres 捕获
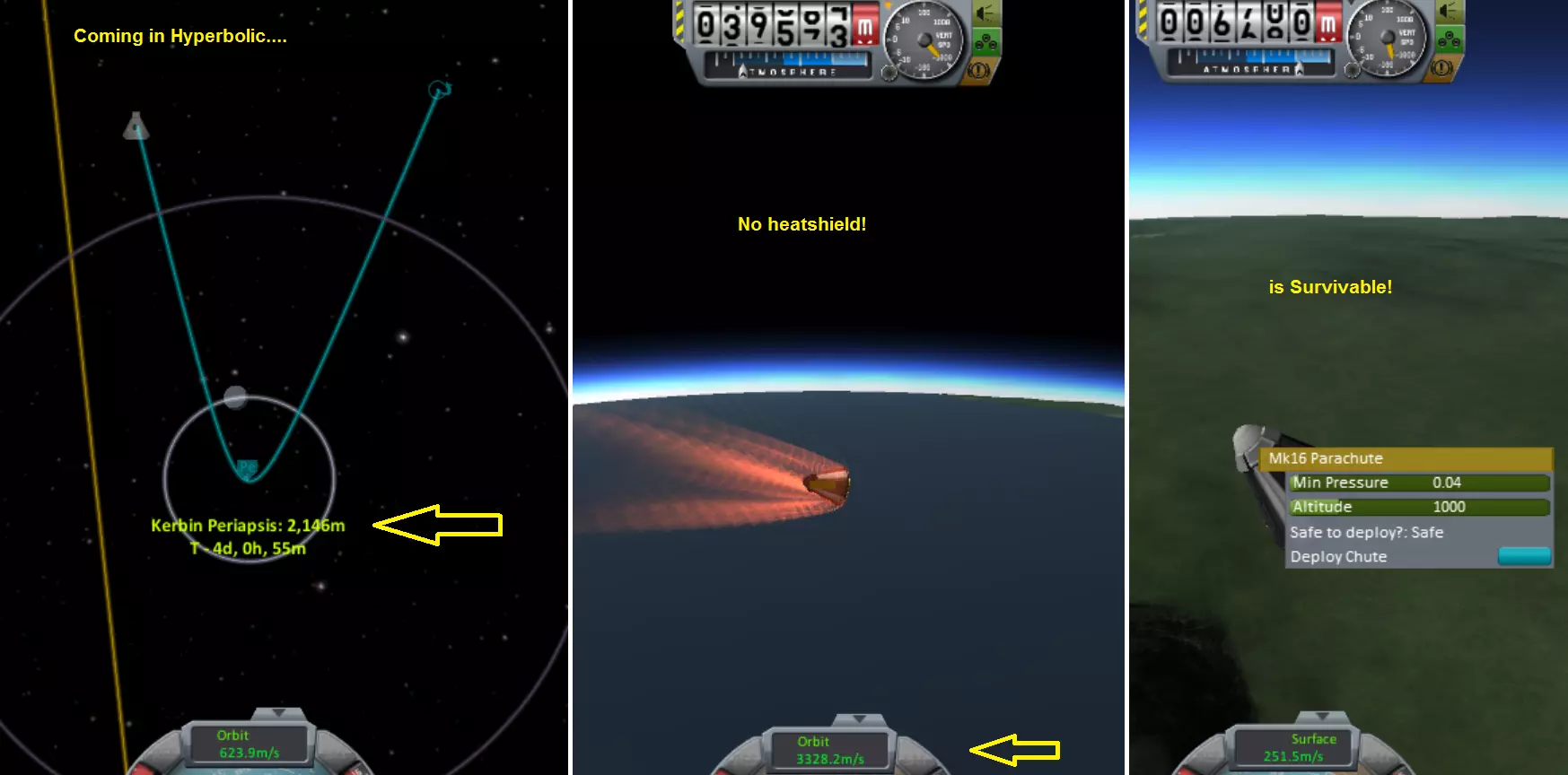
游戏内无隔热罩进行大气制动的截图,以双曲线轨道返回。谁说大角度返回不好?近拱点设置为2千米。
轨道倾角 大多数太阳系中的天体,如行星、卫星等,都倾向于在同一平面内围绕太阳运行。这就是为什么当你仰望天空时,所有行星似乎都沿着同一条路径——黄道运行。 轨道平面存在微小差异,例如火星的倾角为1.85度。在【坎巴拉太空计划】中,【 Dres( Dres )】的倾角为0.6度。 计算从一个轨道平面转换到另一个轨道平面所需的【Δv( Delta - v )】
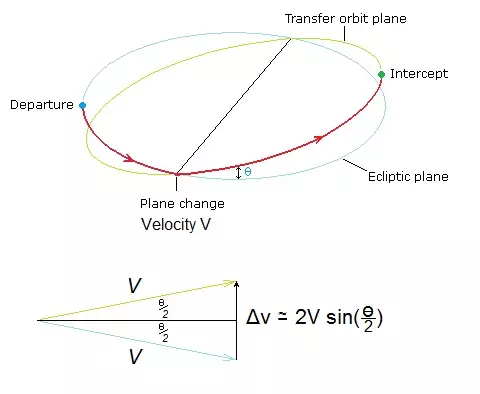
对于小倾角变化,Δν=2V sin(ɵ/2),其中V是轨道平面相交处的椭圆速度。 弹道轨迹 弹道轨迹 当然,如果通过弹道轨迹前往目的地,则无需进行中途修正。 这需要两次倾角变化,一次在出发地,一次在目的地。你可以使用上述公式计算每次倾角变化的Δν,但实际轨迹非常依赖于行星的确切位置,因此没有通用解决方案,这里就不再赘述。
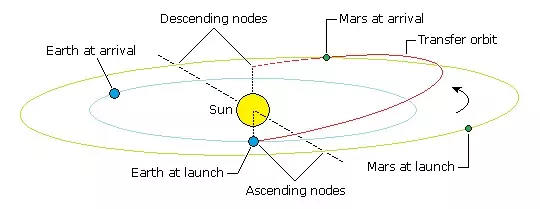
相位角与发射窗口 进行最小能量转移时,必须在特定日期离开Kerbin,否则当你到达Duna轨道时,Duna不会在那里。 相位角是发射时源行星和目标行星相对于恒星的夹角。 对于霍曼转移,我们实际上是从太阳系的一侧前往另一侧。 我们的目标与发射位置成180度角。
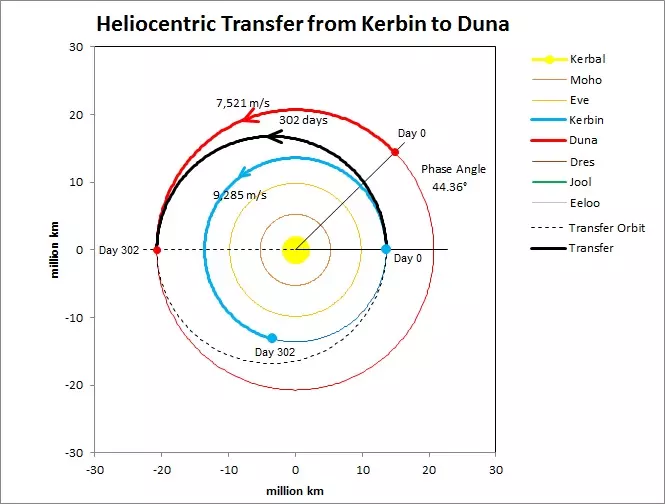
我们可以利用开普勒行星运动第三定律来计算转移轨道以及行星的轨道周期。相位角的计算相当简单。如果转移需要X天,那么我们只需将所有行星的目标位置回溯X天,以找到它们的起始位置。示例4——计算从 Kerbin 到 Duna 的相位角:Kerbol 的引力参数为1.1723328×1018 立方米/平方秒,Kerbin 的轨道半长轴为13599840256米(圆形轨道),Duna 的轨道半长轴为20726155264米(略呈椭圆形),转移轨道半长轴为17162997760米。

TKerbin = 9,203,545秒(426.1天) TDuna = 17,315,400秒(801.6天) TEllipse = 13,048,005.44秒→转移时间= TEllipse/2 = 6,524,002.72秒(302.0天) 那么302天占Duna轨道周期的多少比例? 302天/801.6天×360度=135.6度 相位角为180–135.6度=44.36度 OLEX显示为44.36度。 由于该计算基于圆形轨道的常规运动,而Duna的轨道并非完美圆形,因此存在一定误差。

正圆形的偏心率为0。 《坎巴拉太空计划》中, Dres( Dres)的偏心率为0.05(数据来源于KSP Wiki),因此误差相当小。 实际上,发射窗口通常有大约±5天的时间范围。 示例5 - 前往 Mun( Mun)需要多大的前置角?
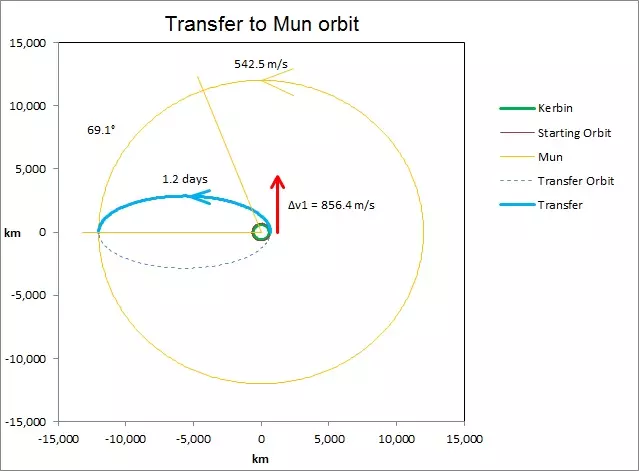
Kerbin引力参数 = 3.5316000×1012 立方米/平方秒 Mun轨道半长轴 = 12,000,000 米(圆形轨道) 转移椭圆半长轴 = (近地点 + 远地点)/2 = (680,000 + 12,000,000)/2 = 6,340,000 米

Mun轨道周期=138,984秒(38.6小时) 转移椭圆周期=53,374秒→转移时间=椭圆周期/2=26,686.89秒(7.4小时) 在7.4小时到达Mun轨道的这段时间内,已知Mun的轨道周期为38.6小时,Mun在其轨道上会移动多远?你也可以使用开普勒方程来计算Mun的轨道周期。 7.4小时/38.6小时×360度=69.1度 仅供参考,如果你要前往Minmus,前置角为65.1度,到达那里需要9个Kerbin日。 ejection angle 坎巴拉太空计划的优点在于它会显示出发轨迹,但如果没有这些便利功能,如何计算在轨道的哪个位置执行第一次“脱离燃烧”以进行星际旅行呢?

本质上,如何计算抛射角η?
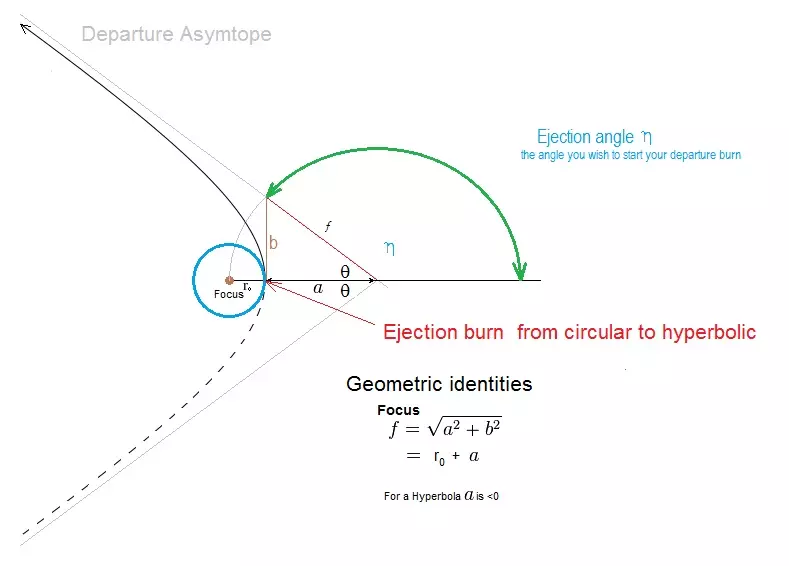
根据上述图片,η=180-ɵ。别问我那个像“n”的奇怪符号是什么,我自己也得查一下。在我们的情况中,它指的是抛出角。或许有某种奇特的亚原子粒子也用这个符号。该死,现在我得去查一下……它叫“伊塔”,存在伊塔介子(η)和伊塔介子素(η′)。不知道能不能用它们作为聚变的催化剂?对于双曲线,a<0,但在以下三角函数恒等式中,我们只使用其绝对值,即|a|。Tan(ɵ)=b/a,ɵ=ATan(b/a),或者Cos(ɵ)=a/f,ɵ=ACos(a/f)=ACos(a/(a+rc)),其中rc是我们初始圆形轨道的半径。
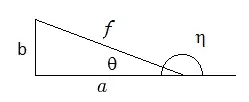
示例 - 出射角 以我们从Kerbin到Duna的变轨为例(即示例3),出射角是多少? 在示例3中,我们已计算出从Kerbin出发的双曲线半长轴为 a = -4,650,267.67米 rc = 80千米高度,即680,000米 ɵ = arccos(a/f) = arccos(4,650,267.67/(4,650,267.67 + 680000)) = arccos(0.8724) = 29.26度 η = 180 - ɵ = 150.74度 Olex显示为151.28度,对于实际应用来说已经足够接近。 总结
航天动力学 Δv Δv(德尔塔-维) 术语“ΔV”有两种常见用法 ΔV - 航天器能够执行的速度增量 ΔV - 执行一次或一系列机动所需的速度增量 计算航天器的ΔV 每个作用力都有一个大小相等、方向相反的反作用力。 火箭燃烧燃料产生高温气体,这些气体从一个方向喷出,从而推动火箭向相反方向运动。

当火箭燃烧燃料时,它会加速。同时,随着燃料的消耗,火箭的重量也会减轻。对于相同的推力,更轻的火箭会产生更大的加速度。 因此,在恒定推力下: - 工作的第1秒,速度变化量为Δv1(米/秒) - 第2秒,速度变化量为Δv2,由于火箭重量略有减轻,加速度会稍大一些,即Δv2>Δv1 - 第3秒,速度变化量为Δv3,且Δv3>Δv2 总速度变化量Δv = Δv1 + Δv2 + Δv3 + …… 通过微分学,我们可以推导出整个燃烧过程中速度变化的通用公式。
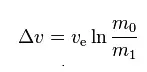

比冲 比冲或比冲量 大多数高中生都熟悉“F=ma(力=质量×加速度)”,但如果一个力在一段时间内持续作用会怎样呢?这就被称为“冲量”。 冲量可以是短暂的,比如高尔夫球杆击打高尔夫球的瞬间;也可以是持续较长时间的,比如火箭发动机的工作过程。 不同固体火箭核心的推力曲线
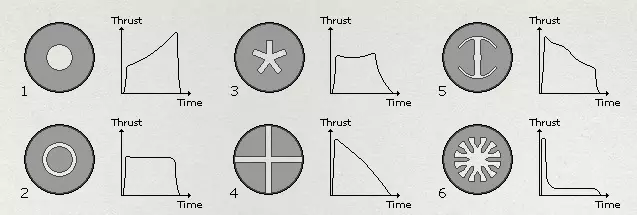
在《坎巴拉太空计划》之外,火箭很少产生恒定推力,因此“总冲量”是推力(力)随时间的积分。 总冲量=∫F dt(牛·秒) 因此,冲量是特定时间内的“平均”力(推力),它等于动量的变化。 比冲(秒)=总冲量(牛·秒)/推进剂质量(千克) 以秒为单位的比冲可用于衡量发动机的效率。可以将其理解为每千克燃料消耗时,火箭能够产生特定推力的秒数。比冲越高,产生特定推力所需的推进剂流量就越低,对于火箭而言,获得特定Δv所需的推进剂也就越少。影响比冲(ISP)的最关键参数包括燃料中的化学能量、燃烧效率以及尾喷管/中心锥的形状。因此,即使两台发动机使用相同的燃料,它们的效率也不一定相同。尾喷管的设计通常会根据其用途和级间分离方式,针对特定压力(高度)来实现最大效率。甚至可能存在除了尾喷管长度外其他完全相同的不同型号发动机。这就是大多数发动机都会分别列出海平面和真空环境下比冲的原因,因为这两个数值可能差异很大。在《坎巴拉太空计划》中,在装配大楼里右键点击发动机可以查看相关信息。压力对排气的影响。
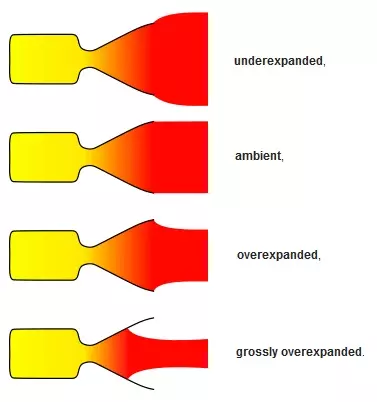
至于燃料,氢/氟组合的能量最高,但由于没人愿意使用氟,我们就退而求其次选择氢/氧组合。液氢/液氧发动机需要昂贵的低温泵和特殊处理,因此许多火箭会使用常温下呈液态的化学燃料。这些燃料可能有毒、具有腐蚀性,而且几乎都具有爆炸性,但这就是火箭科学的特点。典型排气速度 液氧+液氢 4462 米/秒 液氧+煤油(RP-1)3510 米/秒(请注意,大多数地方购买的煤油主要成分是水) 四氧化二氮(N₂O₄)+肼(N₂H₂)3369 米/秒 既然我们在讨论排气速度和比冲
因此,我们的火箭方程可以写成
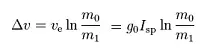
这对《坎巴拉太空计划》来说非常有用,因为每枚火箭的比冲(ISP)数据都会列出(在装配大楼中右键点击部件即可查看),也可以在《坎巴拉太空计划》维基上找到相关信息。
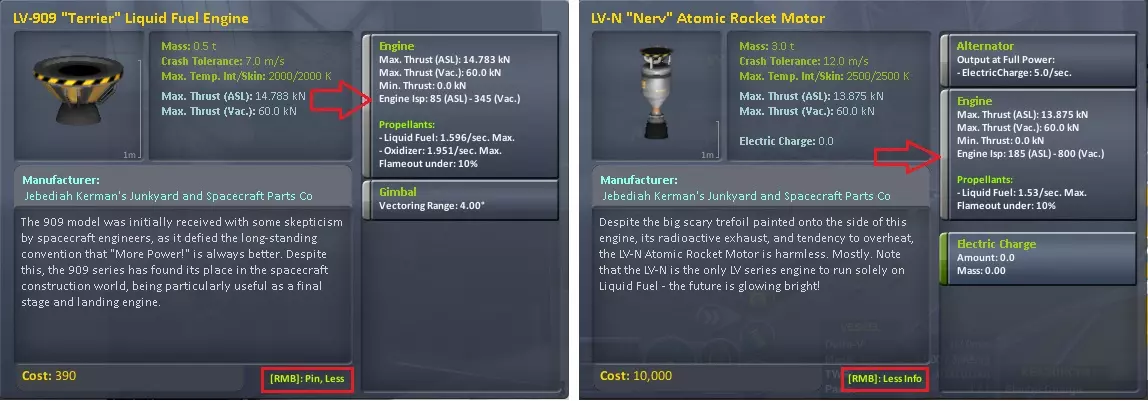
“Nerv”的比冲(Isp)有800!天哪,我要用它来做所有事…… 它也只使用“液态燃料”,所以我可以抛弃所有沉重的“液态氧化剂”,太赞了! 不行 它还重3吨!所以如果你刚才注意听我说的m0/m1,也就是
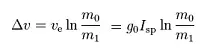
你会明白,只有在搬运重物时才会觉得它非常棒。对于较轻的物品,可以使用像“梗犬”这样的小型引擎。 比冲(Isp)只是衡量引擎效率的指标,而Δv(德尔塔-v)能让你知道可以飞多远。 还有离子引擎,其比冲高达4200秒!(现在用失望的语气说)“但推力只有2千牛”。 别灰心,只要将20个离子引擎串联起来,你就能开始前往其他火箭永远无法到达的遥远地方! 了解一下VASIMR(可变比冲磁等离子体火箭)。比冲可变磁等离子体火箭 以及一些更早期的文章: 《科学美国人》,《太空电推进》,1961年 推重比 推重比是将你送入太空的关键因素。 要从坎巴拉星球发射,你需要推重比大于1。 我通常将火箭的推重比设计在1.6到1.7之间;推重比过高,火箭在发射时容易烧毁;推重比过低,则会在发射过程中浪费大量燃料。 推重比=推力/重量(这应该很明显吧?) 坎巴拉太空计划中,每个发动机都会列出以千牛为单位的推力。1牛顿=1千克·米/秒²(这是一种力的度量单位,是物理学中的力,不是天行者那种力)。1千牛=1000牛顿。 坎巴拉太空计划中,每个部件都会列出以千克为单位的质量。1吨=1000千克。 重量的单位是牛顿?什么情况?没错,是牛顿。 重量=质量×当地重力常数g 你可能会说自己重80公斤,但从真正的物理学角度来说,你的重量其实是80×9.80665=784.5牛顿。(别想太多) 在火星上,当地重力仅为地球重力的0.376倍,你的重量就是0.376×784.5=285牛顿。此时你的重量是285牛顿,但质量仍然是80公斤。 在太空中,推力重量比(TWR)基本无关紧要,因为火箭效率和Δv才是你应该主要关注的。TWR或者更准确地说推力质量比(因为在太空中没有重量),会决定完成特定机动所需的时间。 低推力质量比意味着完成机动需要更长时间,长到可能使一些时间关键的机动变得无法完成。高推重比意味着你的燃烧时间会短得多,这可能意味着由于人类按按钮的局限性,你无法足够精确地控制燃烧持续时间来进行精细操作。 如果我需要推重比大于1才能从坎星起飞,那么从 Mun 起飞需要多少推重比? 理想情况下,你需要推重比大于1,因为你的重量是本地的,但如果你使用 KER(Kerbal Engineer Redux),它会根据坎星来计算所有数据。 根据坎巴拉太空计划维基,Mun 的本地重力为0.166g。 因此,要从 Mun 起飞,你需要推重比大于0.166。 这只是为了起飞,如果你想及时完成,可能需要更大一点的推重比,比如:推重比=1.65×0.166=0.由于 Mun 没有大气层,你无需担心起飞时的烧毁问题,因此除了操控方面的问题外,没有实际的上限。 燃烧时间 执行一次机动需要多长时间?坎巴拉太空计划的导航球会显示,但如何计算呢? 这并不难,只是有点复杂。 燃烧时间(秒)= 所需燃料(千克)/ 推进剂流量(千克/秒) 所需燃料(千克) 即特定Δv(德尔塔V)机动所需的燃料量。 m1(最终质量)= m0(初始质量)– 所需燃料质量(mf) 代入火箭方程,经过一些运算后我们可以得到。
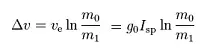
通过一些替换和操作
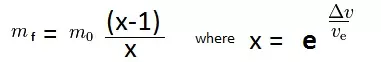
推进剂流量(千克/秒) 通常人们不会计算流量,而是在实验室中测量,但在《坎巴拉太空计划》中无法这样做。 你可以根据火箭的比冲来确定流量。 推进剂流量(千克/秒)= 推力(牛)/ 排气速度(米/秒) 从《坎巴拉太空计划》v1.1版本开始,游戏会显示每个发动机的消耗率以及每个燃料箱的容量。 要计算最大燃烧时间,只需用燃料总量除以发动机流量。 最大燃烧时间=所有燃料箱总量/发动机流量 【注:当FL-T400燃料箱显示有220单位燃料和180单位氧化剂时,这里的“单位”并非指升,实际上其具体单位并不明确,似乎是与重量相关的衍生单位。】900千克液体氧化剂/5→220单位液体氧化剂。仅供参考,液氧的密度为1.14千克/升。示例 - 确认坎巴拉工程师Redux的计算结果
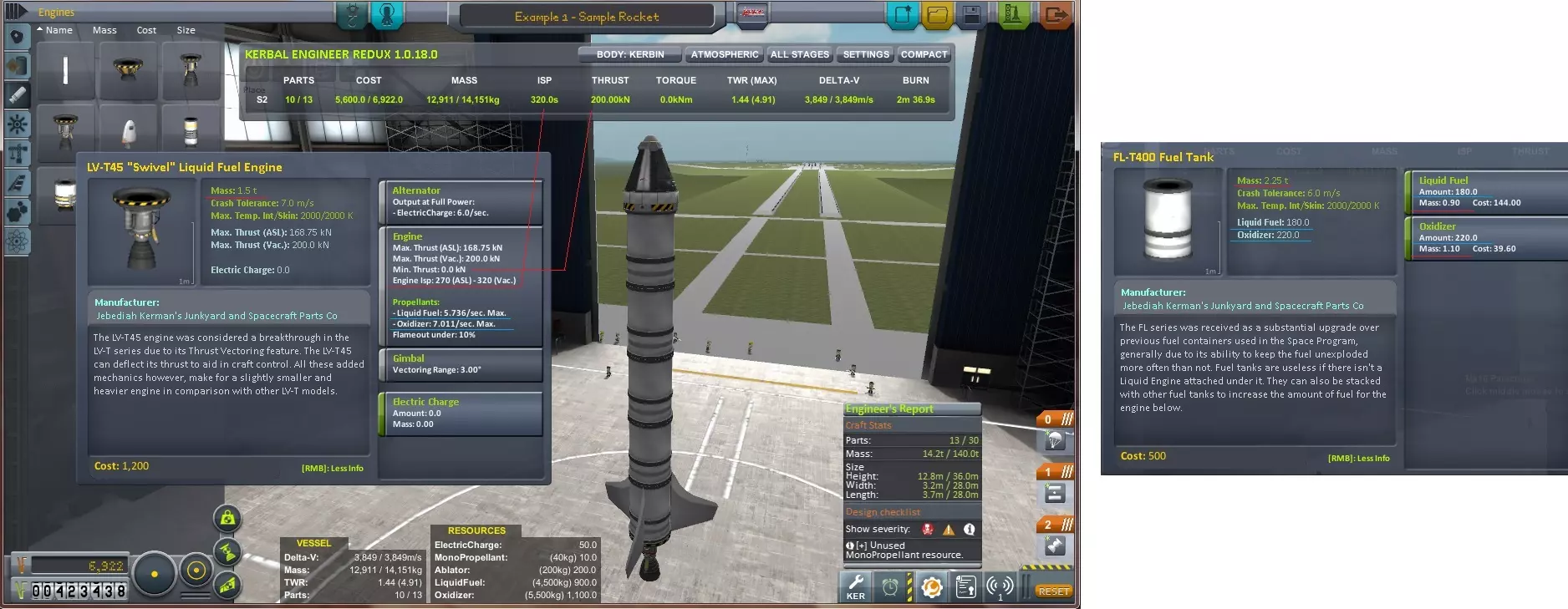
[/previewicon]
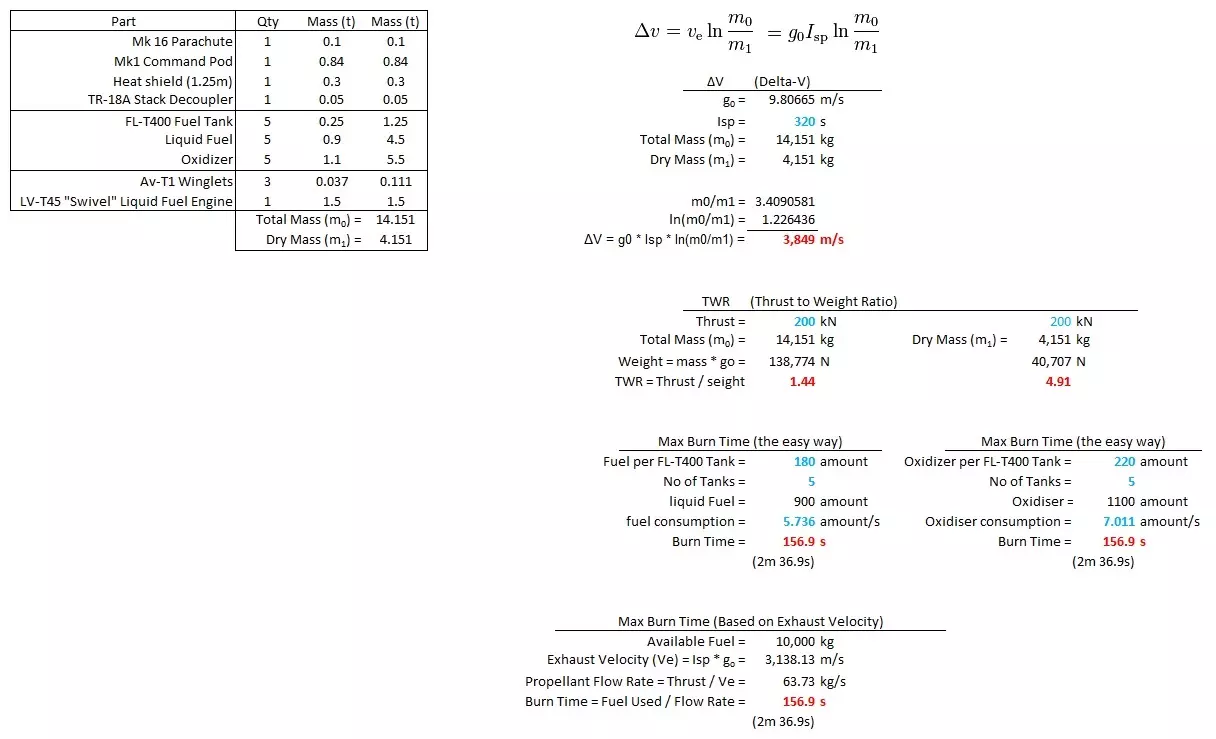
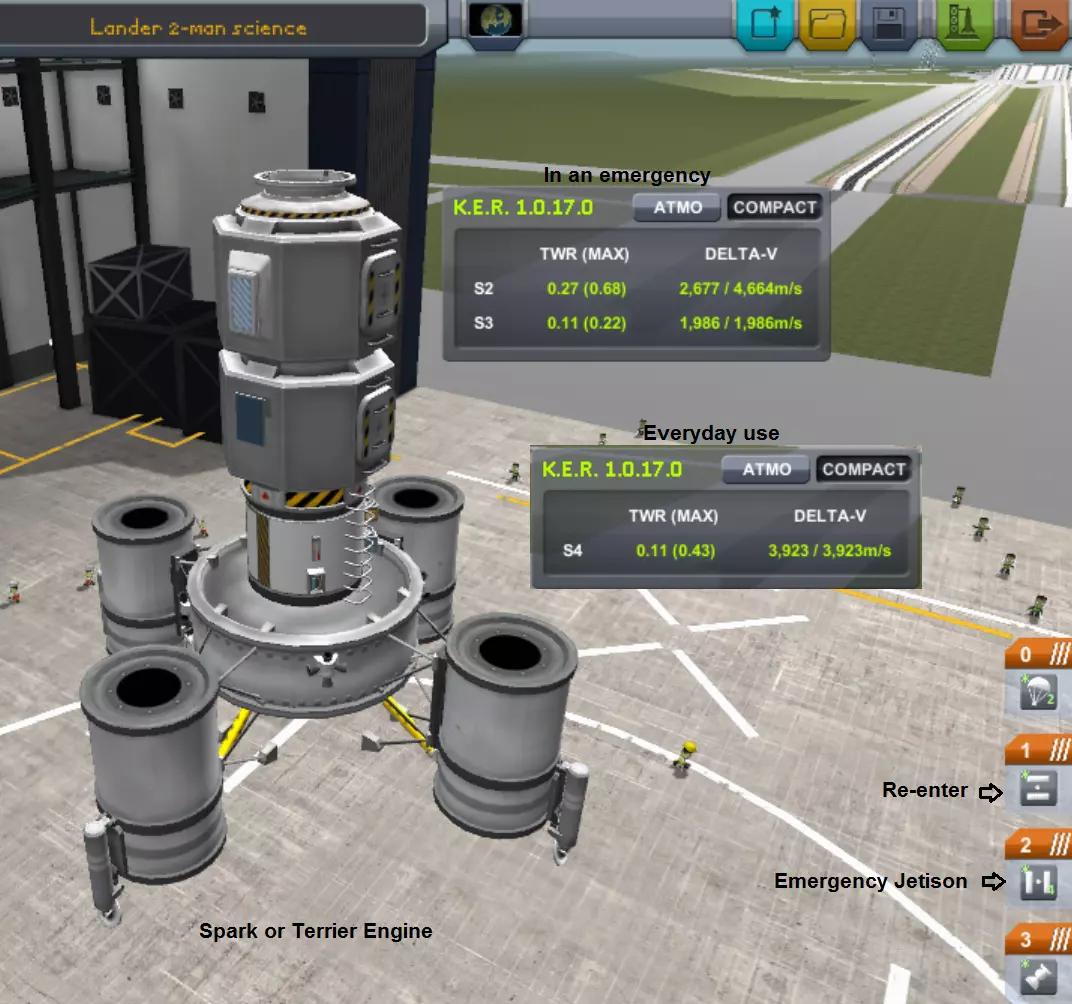
致《坎巴拉太空计划》工程模组重制版的开发者们,感谢你们制作了这个优秀的模组。 示例:我能回家吗? 我能安全返回地球吗?或者我还剩下多少【ΔV】?
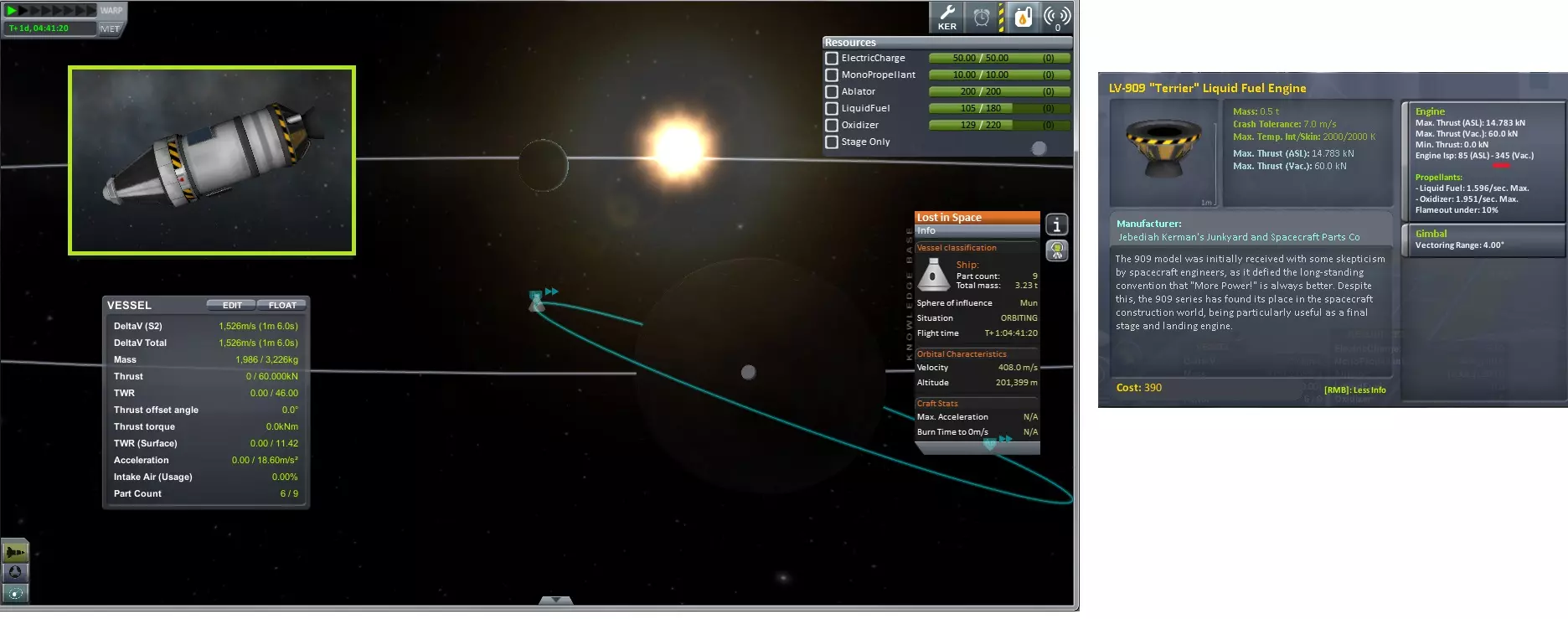
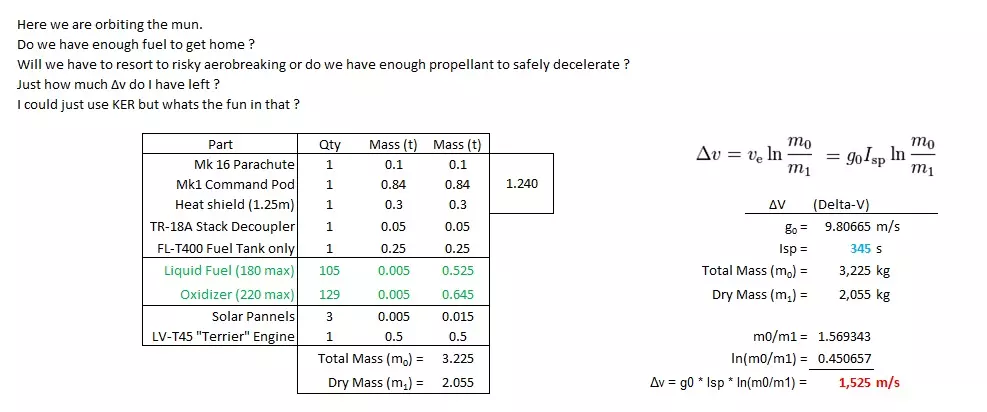
这和KER的数据基本一致。在《坎巴拉太空计划》中,推进剂的重量为5千克/单位。我们可以直接从资源选项卡中读取剩余的推进剂单位数量。火箭设计包括分级等内容。
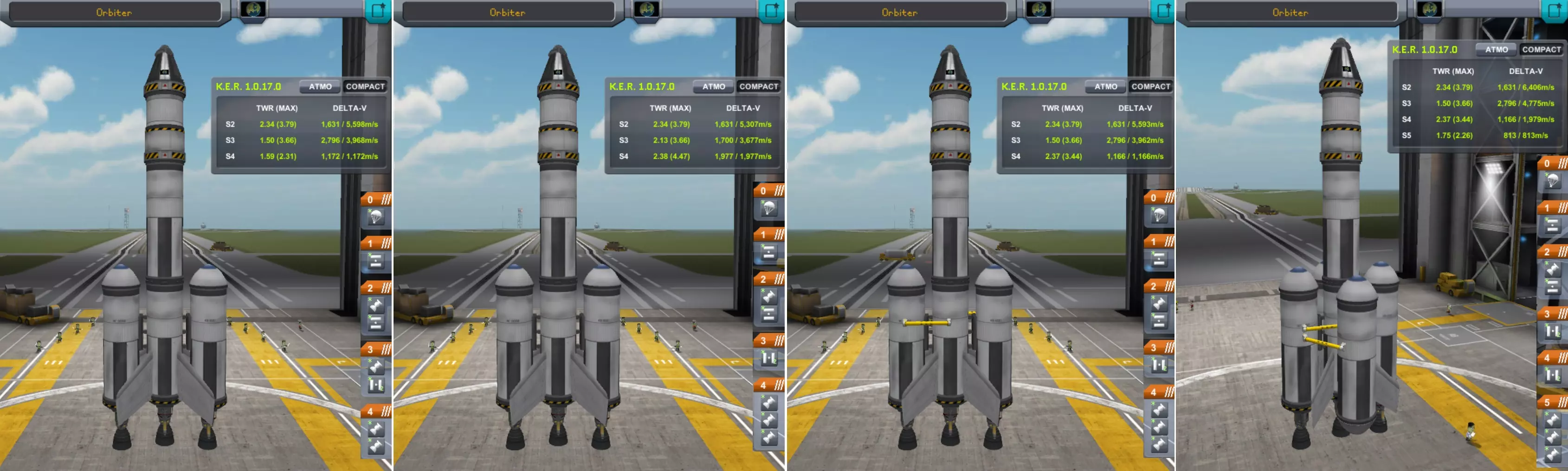
1 - 晚期分级.......... delta-v(Δv)= 5,598米/秒,推重比(TWR)1.59 2 - 早期分级.......... delta-v(Δv)= 5,307米/秒,推重比(TWR)2.38 3 - 交叉输送.......... delta-v(Δv)= 5,593米/秒,推重比(TWR)2.37.......... 兼具两者优点 4 - 燃料舱.......... delta-v(Δv)= 6,406米/秒,推重比(TWR)1.75 四 asparagus 级用于你想去往其他地方时....
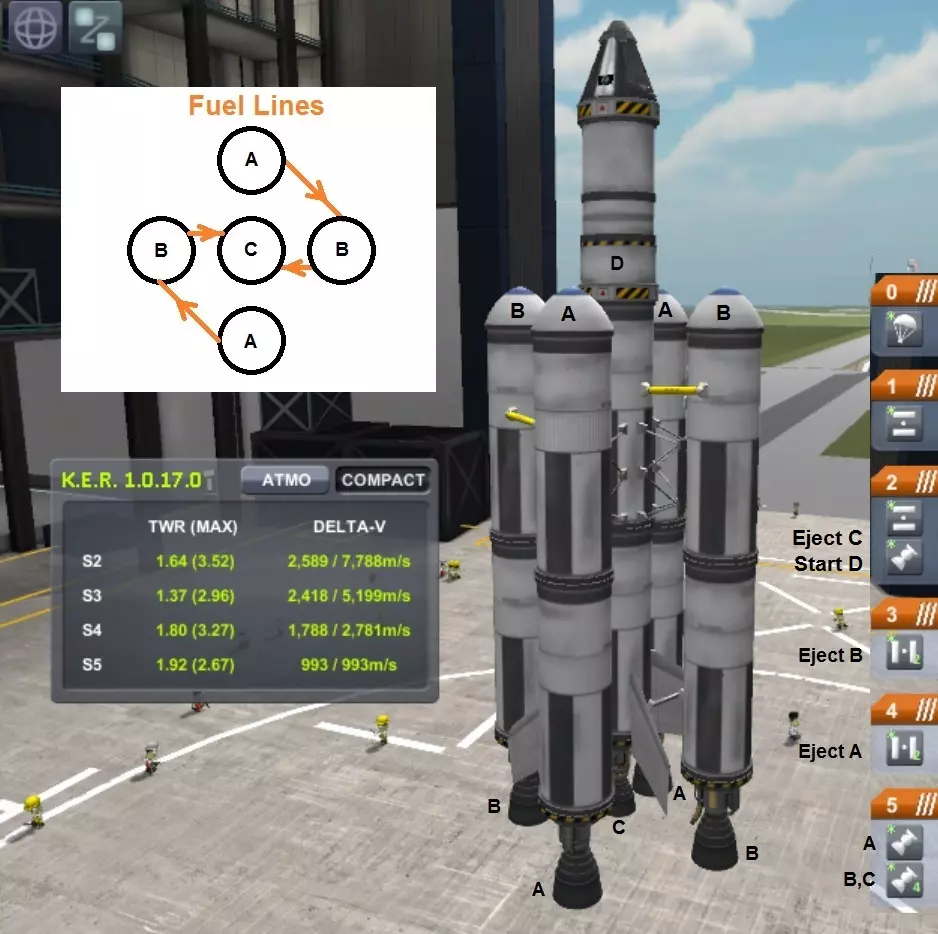
关于芦笋式火箭的更多技巧:6 两个单人舱比一个双人舱更轻。 飞行员和科学家团队进行多次生物群系跳跃是获取科学点的好方法。 让你的科学家收集所有科学数据,并在每次调查之间重置设备。 在太空中对接加油,返回坎巴拉星球时仅用两个座舱再入大气层。

聊聊扭矩——充分发挥推进器的性能
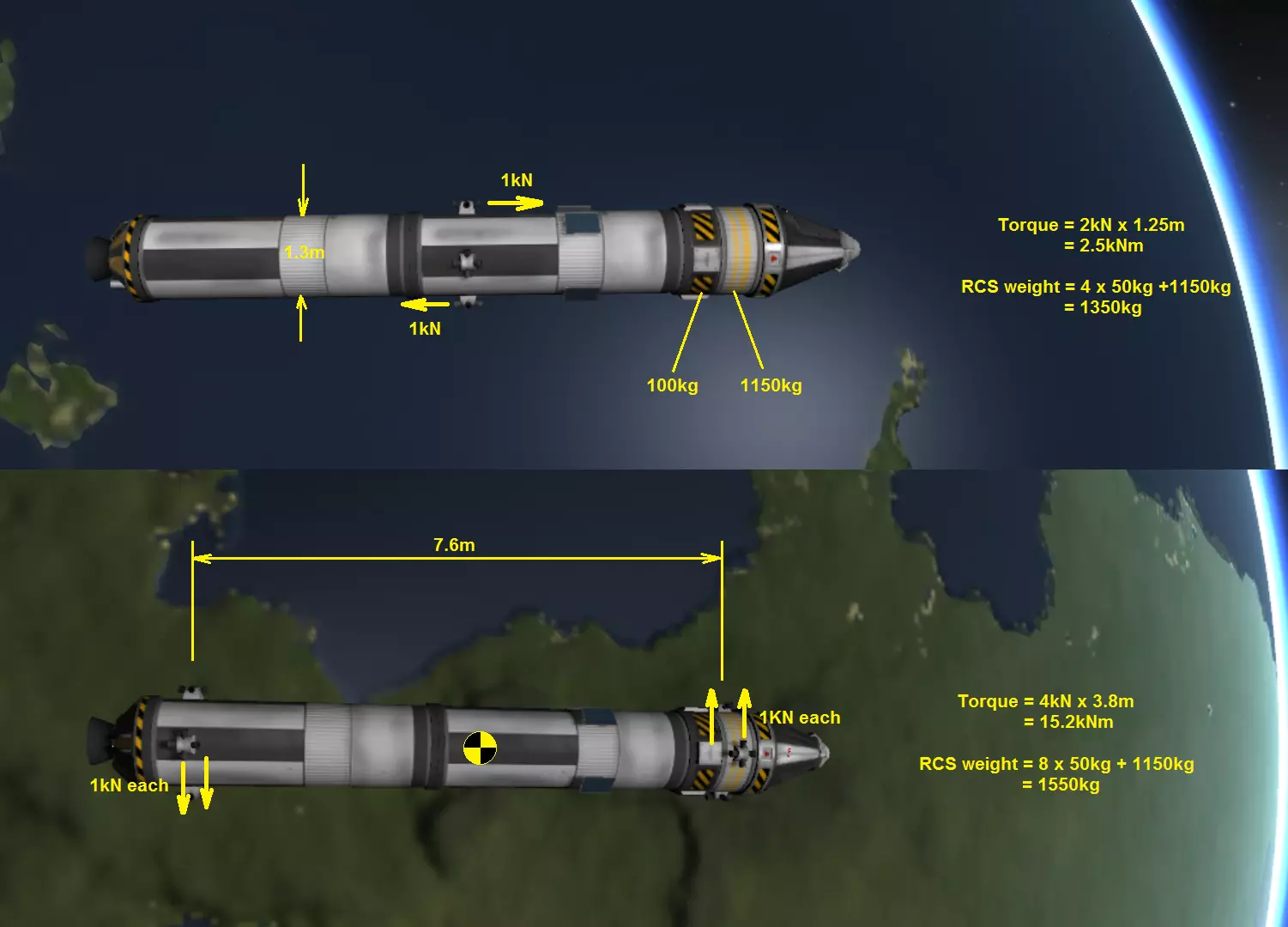
注意推进器很重,我通常只在需要横向推力进行对接的航天器上安装它们。 小型内置反作用轮重50千克,可产生5千牛·米的扭矩。 高级内置稳定器重100千克,可产生15千牛·米的扭矩。 高级反作用轮重200千克,可产生30千牛·米的扭矩。 火箭稳定性
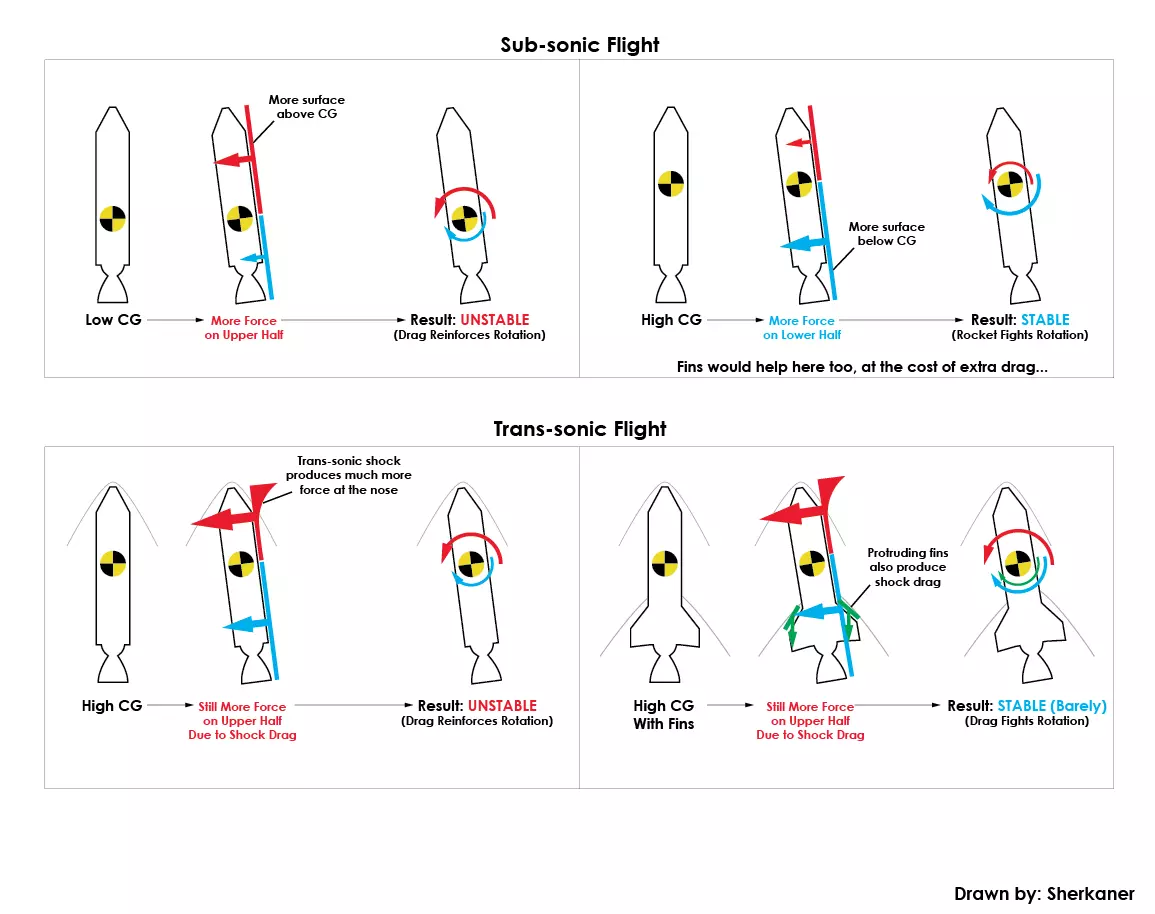
靠近时看起来平平无奇......
一些实用的在线计算器 轨道力学 火箭推进 我的资料
ć°ĺŚ
2026-02-20 13:00:14 发布在  Kerbal Space Program
Kerbal Space Program
说点好听的...
收藏
0
0