“At first I think it is Civilization 4 in Space. After a while, I feel like that I am reading Das Kapita, by Karl Marx. As the game go on, my mind is occupied by The Wealth of Nations, by Adam Smith. In the end, I am as mad as Jesse Livermore from Reminiscences of a Stock Operator. ” In this guide, I will teach you how to calcuate the price of differenct resources and also offer a tool, in excel, to help you calculate it yourself. Finally, I would gives some advices of how to exploit this knowledge against AI, the purpose. Section I : Labor Theory of Value The labor theory of value (LTV), usually associated with Marxian economics, argues that the economic value of a good or service is determined by the total amount of "socially necessary labor" required to produce it. Often this is expressed mathematically as: C + L = W Where: C is the constant capital of materials used in a period plus the depreciated portion of tools and plant used in the process. (A period is typically a day, week, year, or a single turnover: meaning the time required to complete one batch of coffee, for example.) L is the quantity of labor time (average skill and productivity) performed in producing the finished commodities during the period W is the value (or think "worth") of the product of the period ( w comes from the German word for value: wert) To put it in simple world: Value of Input + Value added by Labor = Value of Output Where, Value of Input include raw materials and upkeep for buildings and peoples. Section I: Labor Theory of Value in Stellaris Without any modifiers, a technician job cost 1 Food and 0.25 Consumer Goods for upkeep and produce 6 Energy per month, in Stellaris. If we apply Labor Theory of Value on a technician, we can get the following equation from a Technician Job. 1F + 0.25C + 1P = 6E. Where: F is Food. C is Consumer Goods. P, short for PoP, stands for the labor value of a technician per month. E is Energy.Don't forget that the labor value, P, should be added with the value of input to get the final value of job's output. Value of Input + Value added by Labor = Value of Output Here is the full version of equation, completed with a bunch of 0 inputs. These inputs is zero in this case but not necessary be 0 in other circumstance, for example power plant increase the output of your technician by 1 but require 1 strategics resource for building upkeep. So it is a good practice to list them all, even when they are 0. 0E+0M+1F+0.25C+0A+0S+1P = 6E Where: E is Energy. M is Mineral. F is Food. C is Consumer Goods. A is Alloy. S is Strategic Resource. P, short for PoP, stands for the labor value of a technician per month. I do not count for modifier and upkeep for building and district in the above equation. Things like these will be covered in section II. In this section, we are just discussing the general theory and principle, so a simplified example is offered. In Labor Theory of Value, the labor value is the same for every one, no matter who you are. Therefore, the labor value per month of a ruler is the same as that of a slave. I don’t know about real world economic, but I believe it is true in Stellaris. A PoP is a PoP. I do not care about its social status. For me, every PoP certainly has the same labor value per month. Therefore, we could apply the same Labor Theory of Value rule into different jobs and we could get a bunch of equation from each resources job. Every job, regardless of their social status, has the same labor value per month, which means they all have the same P in equation. Remember that P stands for the labour value per month of a PoP. Technician: 1F+0.25C+1P = 6E Miner:1F+0.25C+1P= 4M Farmer:1F+0.25C+1P = 6F Artisian:6M+1F+0.5C+1P = 6C Metallurgy:6M+1F+0.5C+1P = 3A Strategic Resource: 10M+1F+0.5C+1P = 2S And below is the full version of equations, by adding back those 0 inputs. Technician: 0E+0M+1F+0.25C+0A+0S+1P = 6E Miner:0E+0M+1F+0.25C+0A+0S+1P= 4M Farmer:0E+0M+1F+0.25C+0A+0S+1P = 6F Artisian:1E+6M+1F+0.50C+0A+0S+1P = 6C Metallurgy:0E+6M+1F+0.50C+0A+0S+1P = 3A Strategic Resource: 0E+10M+1F+0.50C+0A+0S+1P = 2S If you do not skip your math class, you can easily solve a group of equation like the below: x + y =13 2x - y =2 The equation group we get from Stellaris look daughting, but it is still easily solvable. Nowaday we let computer do the calculation instead of ourself. And, here is the result: 1 Mineral = 1.5 Energy 1 Food = 1.0 Energy 1 Consumer Good = 2.6 Energy 1 Alloy = 5.2 Energy 1 Strategic Resource = 10.8 Energy 1 month of labor value of a PoP = 4.3 Energy The above result is very similar to the market price in Stellaris. Because the market price of mineral is just 1.3, lower than its true value, therefore, players tend to buy in mineral from the market at the very start of the game. Conclustion To sum up. In this section, we learn that we could easily get the true value, or trading price in energy, for various resources by applying LTV theory and solve a group of equation. And the result is very satisfying, since it is valid and has a sound economic theory behind it. 1 Food trade for 1 Energy, because they both have the same efficency, that is, 1 PoP produce 6 Energy or 6 Food with the same upkeep. 1 Mineral trade for 1.5 Energy, because 1 PoP produce only 4 Mineral instead of 6 Energy with the same upkeep. Yeah, that is law of the value of commodities from Karl Marx for you, in case you skip your economic lesson during class. Law of valueThe law of the value of commodities (German: Wertgesetz der Waren), known simply as the law of value, is a central concept in Karl Marx's critique of political economy.Most generally, it refers to a regulative principle of the economic exchange of the products of human work, namely that the relative exchange-values of those products in trade, usually expressed by money-prices, are proportional to the average amounts of human labor-time which are currently socially necessary to produce them within the capitalist mode of production. Simply put, if product A takes 100 hours of human work to produce in total, and product B takes 5 hours to produce, the normal trading-ratio of A and B will gravitate to a rate of around 1:20 (one of A is worth 20 of B), because A is worth much more than B. Section II: Calculator If you are as lazy as me, who do not want to do the calculation work, here is the good news for you. I create a excel file to do the calculation of Section I and this calculator could count for modifier and district and building upkeep. The file look like this.

你需要做的是：将《群星》中的数据填入绿色区域A3:G8和H3:M8。绿色区域A3:G8为岗位提示框中的数据，绿色区域H3:M8为区划和建筑的数据。 将橙色区域P3:W8的数据复制到Octave中并按Enter键。然后将橙色区域Y3:AA9的数据复制到Octave中并按Enter键。Octave会为你进行计算。 将Octave中的结果复制并粘贴到红色区域AD3:AD8。 享受计算出的各种资源以能量币为单位的价格吧。 我会选择我的一个后期存档（2355年）作为示例来指导你完成此过程。 第二部分：填写绿色区域A3:G8和H3:M8 以技术人员为例，游戏内岗位提示框显示其产出24.5能量币，消耗1.1食物和0.2消费品。我们在单元格B3中填入24.5，-1。C3单元格为1，E3单元格为-0.2。正值表示产量，负值表示成本和维护费用。

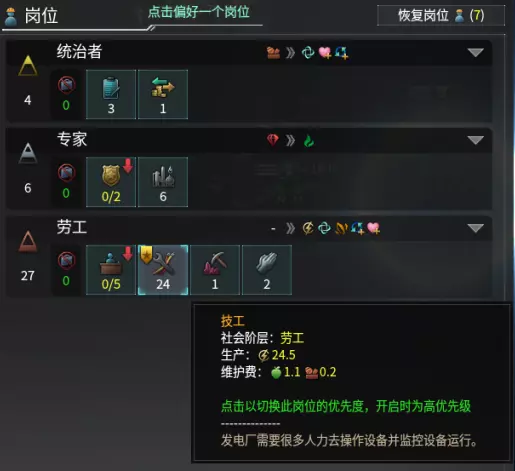
补充说明：由于一项以消耗食物为代价提升增长率的法令，我的食物维护费用为1.1。由于一项能降低人口、区域和建筑维护费用10%的传统，我的消费品维护费用为0.2。 一名技术人员需要电力区域和发电建筑来获得工作岗位并提升产能。电力区域消耗0.9能量币并提供2个工作岗位。发电建筑的维护费用为1.8能量币和0.9稀有资源，且该维护费用由24名技术人员共同承担。因此，我在单元格H3中填入“=-0.9/2-1.8/24”，在单元格M3中填入“=-0.9/24”。

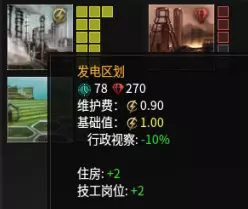
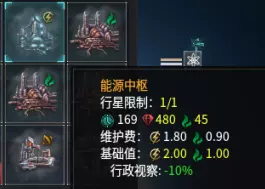
你对其他工作也照此操作即可。 附：工匠岗位的B6单元格之所以有+2能量，是因为我拥有“大师工匠”文明特性，该特性为工匠提供+2贸易值，而这些贸易值可转化为+2能量。 附2：单元格内容为“产出 - 维护费用”。例如，在D5单元格中，我的公式是“=-1.1+30.1”。其中-1.1是人口的食物维护费用。之所以是-1.1，是因为我有一项法令，该法令使食物维护费用增加10%，同时提升人口增长。30.1是我的农民的食物产出。 附3：哦，对了。我是中国人。这就是为什么这份指南中有这么多语法错误，以及我对马克思主义经济学和数学如此熟悉的原因。 附4：在你提问之前，是的，我也是一名共产主义者。来抓我呀。^ ^ 开个玩笑。我们在学校学习共产主义，但没人把它当回事。其背后的理念宏大且富有野心，但遗憾的是并不实际。要让共产主义成功，每个人都得是圣人。可我们都只是普通人，有着自己的利益和欲望。这就是为何在伟大理念之下会滋生出如此多的错误行径。 “自由啊，多少罪恶假汝之名而行！”——罗兰夫人 第二部分：将橙色区域的数据复制到Octave中 橙色区域的数据有两个用途。 第一，汇总绿色区域的所有成本、维护费用和产量。 第二，将数据整理成Octave能够识别和计算的格式。 Octave[octave-online.net] 将橙色区域P3:W8的数据复制到Octave中并按回车键。

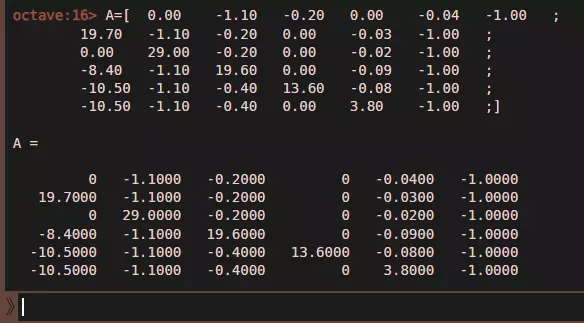
然后将橙色区域Y3:AA9的数据复制到Octave中并按Enter键。

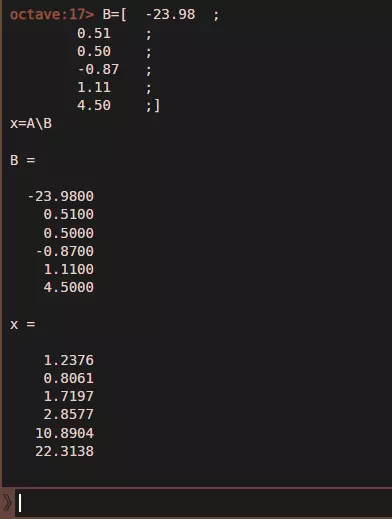
第二部分：将Octave的结果复制并粘贴到红色区域AD3:AD8。复制“x =”行下方的数据，如图中高亮区域所示。

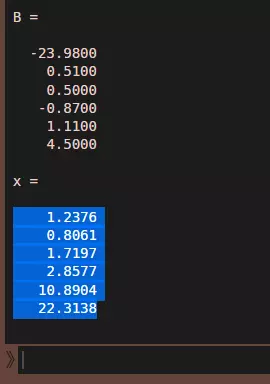
附：它被高亮显示是因为我选中了它，这样我就能复制了。 第二部分：查看你各种资源以能量计算的价格。 这是最终结果。在这款游戏中，1单位矿物价值1.2能量，因为矿物的生产效率不如能量。1单位食物价值0.8能量，这是由于我发现了一颗拥有40%食物生产加成的星球。以此类推。

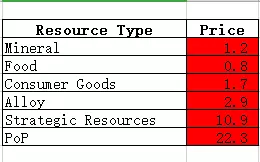
附：如果你比较懒，可以跳过填写绿色区域H3:M8中对应区域和建筑维护费用数据的步骤。根据我的测试，结果非常相似。下图展示了两种结果，右侧列是未计入区域和建筑维护费用的结果。

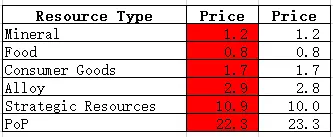
原因在于建筑的维护费用由众多人口分担，因此最终费用极低。区域的维护费用在初期就很低。 第三节：绝对优势 绝对优势指的是个人、公司、地区或国家在单位时间内，以相同的投入量能生产出更多数量的商品或服务，或者在单位时间内生产相同数量的商品或服务时使用更少投入量的能力，相比其竞争对手而言。 绝对优势的概念由亚当·斯密在《国富论》中提出，旨在说明各国如何通过专门生产并出口自己比其他国家更高效生产的商品，同时进口其他国家更高效生产的商品来获取利益。专注于并交易本国具有绝对优势的产品能使两国都受益。 一般来说，能源比矿物更高效。3.5版本更新后，新增的星球自动管理功能接受以能源作为原材料来建造建筑。因此，这极大地提升了能源的实用性，并主要减少了矿物在合金和消费品生产中的使用。而且，采矿站能产出大量矿物，且无需劳动力。这就是为什么只要AI提供的汇率比玩家自己生产更划算，玩家专注于只生产能源并尝试从AI那里交易矿物是个好主意。 第三节：金融资本 “知道股票价值的人总会在股价处于低价时买入。”从金融资本的角度来看，《群星》中有三种获取价值的方式。 第一种是通过雇佣人口（Pop）进行生产来创造价值，这与现实世界的制造业运作方式类似。 第二种是通过投资获取价值。投资时，你预先支付成本，然后随着时间推移获得回报。宣称星系主权或建造太阳能电池板 starbases 都属于投资，它们不需要劳动力，资本自身就能产生价值。 最后一种并非通过创造或投资，而是通过贸易利用资本本身从无到有地获取利润。你进行的贸易越多，获得的利润就越多。通过这种方式，你基本上是利用资源价格的信息不对称来“掠夺”AI。市场 由于能源生产比矿物生产效率更高，矿物的价格总是高于能源。因此，玩家常用的一个技巧是每月从市场购买50单位的矿物，这比自己生产矿物更划算。 当银河市场开放时，只要有利可图，我就会大量买卖商品。如果合金价格很高，比如8能源，我就会出售合金。通过计算，我能准确知道哪个价格对我来说是有利可图的。依赖外部资源存在风险，因此我会尽量保持较高的库存。 与AI交易 我们也不会止步于亚当·斯密所建议的与AI达成双赢贸易协议。我们将所有资源都作为资本，一心为了获取利益而进行激进的贸易。赌博时，知晓结果的一方总能获胜，而你拥有我的资源真实价值计算器，自然掌握着这类信息。 《群星》的AI往往会过高地评估食物、战略资源和矿物的价值。因此，我非常喜欢向AI出售战略资源，偶尔也会卖些食物。由于我自己很少生产矿物，所以一直很缺矿物，也就不可能出售进口的矿物。 用100单位战略资源换取4110能量币，相当于以41.1能量币的单价出售战略资源，这个价格实在太高了。

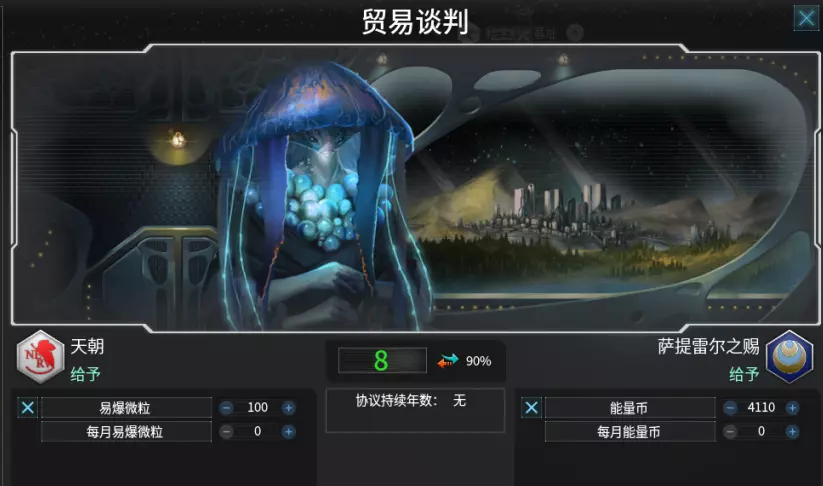
进行激进贸易战的一个有效策略是，你可以向AI大量交易你的战略资源，将它们的能源/矿物储备和每月收入逼至接近零。你要买下它们所有的现有库存以及未来30年的产出。通过这种方式，它们的经济会陷入瘫痪。它们没有足够的能源或矿物来维持日常消耗，不得不将从你那里买来的战略资源拿到市场上出售以换取能源或矿物。 然而，它们一开始接受与你达成的不利交易就已经注定了失败。我发现，经常与我进行贸易的AI很快就会实力衰退。 其次，当它们被迫在市场上出售资源时，价格会下跌，你就能以更低的价格买回刚刚卖给它们的战略资源。你获得了双重胜利。 PS：本指南撰写于《群星》3.6版本时期。