Your NEW go-to Daily Tidy Calendar Guide :-) Completely reworked to include all the possible variations for this puzzle type, after the June 2025 Game Update. ------------------------------------------- (published now as 'almost finished' to help people with the 28 August Calendar Daily Tidy. The guide is mostly done, but still needs some polishing, some more screenshot examples, and a fleshed-out chapter 4 on Pattern Matching. All coming soon !) ------------------------------------------- The Guide is split into separate Chapters, providing different levels of guidance and hand-holding. Chapters 2, 3 and 4 are made so that they can be read as standalones. BUT do look at Chapter 1 and the 'Definitions' section, first. Chapter 1 explains the basic structure of the puzzle type. Plus some helpful hints. No spoilers. Chapter 2 gives text descriptions to help you understand the logic of solving it 'for yourself', and some examples to show some of the variations you can get, and ways to think through to the solutions. Some spoiler-ish info. Chapter 3 is a prescriptive step-by-step that will lead you to the solution for all puzzle variations. Just give yourself a little time to sit down calmly and follow each step, and it will give you your solve :-). Spoilers. Chapter 4 is for the Pattern Matching method. I've got some text in, but not step-by-step screenshots yet. Coming soon.... And I intend to include some more examples in an 'Extras' section right at the end, but that is work in progress too, as yet. NOTE that people's heads work differently. And what might be obvious and intuitive for some people, may need more hand-holding and detailed explanations for others. This guide tries to meet people's needs broadly, and to provide guidance that will work for all puzzle variations. So please have patience, if perhaps you feel like it's too detailed for you in places ;-) It's not a difficult puzzle type, once you've got your head around the logical structure of it. Really ! So give yourself a bit of time to sit down with it and work it through without rushing, and I'm confident it will all seem a lot easier than at first glance. Chapter 1: Main principles This is a simple repeating-pattern puzzle. How to solve: On your starting calendar, there is always at least two stickers of the same type (a "Starting Double"). Look at how many stickers of this type are still waiting to be placed. Place those stickers onto the Calendar so that they are evenly spaced out, with the same interval (same number of days) between every one of the stickers of the same type. That was the harder bit of the puzzle. Now the rest is easy: -- Place all your other sticker sets onto the Calendar too, using the same interval (same number of days apart) that you found for your first sticker set. OR -- Use 'pattern matching' for the rest of your stickers. SOLVED ! REMEMBER: You CAN place more than one type of sticker onto the same day, if you need to! NOTE: Only one repeat pattern for your Calendar, not different intervals for different sticker sets. You can only use days 1 - 31 on your Calendar. There is no last month or next month. All stickers must be placed onto the Calendar. Practical hints:There may be more than one Starting Double on your Calendar. You get the same solution whichever one you choose to start with. BUT it is usually easier to see the solution if you pick the Starting Double with the shortest gap between the two stickers in the Double. Sticker sets can be anywhere between 2 and 7 stickers in total, counting together both the sticker/s already on your Calendar at start AND the ones of the same type waiting outside the Calendar. All the sticker sets for your Calendar will be similar in size. (NB. This is new since August, when the 'big sets+small sets' variation was removed). You are looking for a repeat pattern of somewhere between a 5-day and a 15-day interval. Logically: You will need a longish interval if you have small sticker sets with few stickers. And a shortish interval if you have large sticker sets with many stickers. And don't forget that the interval has to fit with the gap between the two stickers in your Starting Double, too. You will often have to place more than one sticker type onto the same day on the Calendar. Especially if you get a Calendar with large sticker sets. Make sure that the centre of each sticker is properly inside the date box, otherwise it won't register properly. You can overlap stickers or place them right on top of each other if you need to, to get them all to fit into the date box. Some people solve this by 'doing maths' in their heads, others by counting day-by-day directly on the calendar, others again perhaps by trying out different intervals and just seeing which will fit. Whatever way you use to solve this, DO make sure that you haven't mis-counted anywhere. If your puzzle won't solve, often it is because of a simple mis-count on the Calendar, and not because your thinking was wrong. A few definitions: Just to be clear what is meant by certain expressions in this guide a "Starting Double" : 2 stickers of the same type (i.e. identical icons) that are already placed onto your Calendar at start. There will always be at least one Starting Double for your Calendar. a "sticker set" : all stickers of the same type (i.e. identical icons). Counting together the sticker/s of that type already on your Calendar and the stickers of the same type still waiting to be placed. "X days apart" : the number of days between two stickers of the same type. Example: if one sticker is on 4 and the other on 8 : that is 4 days apart. Example: if one sticker is on 3 and the other on 28 : that is 25 days apart. "repeat pattern" : the spacing that works for a sticker set so that all the stickers are evenly spread out over the Calendar, with all the stickers in the set placed the same number of days apart from each other. The number of days between the stickers in the repeat pattern is also referred to as 'interval' and 'repeat interval' in the guide here. Note: that the repeat pattern that works for one sticker set, will work for all the other sticker sets on your Calendar too. Chapter 2: How-to: simple guide, with some examples xoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxox The examples in this chapter (see following section) all follow the same puzzle logic, but have been chosen to show a few different variations you can get, and ways to think about the solution. If you find you need more detailed step-by-step guidance than you get in this Chapter, then go look at Chapter 3 in this guide. xoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxox First of all, look at your Starting Double and the sticker set it belongs to. It will give you your solution !REMEMBER that you are looking for a pattern of somewhere between a 5-day and a 15-day repeat. Nothing longer or shorter than that. To fit all stickers in a set on with equal number of days between them, you will need a long repeat interval if you have small sticker sets, and a short repeat interval if you have large sticker sets. And the repeat interval also has to fit with the 'X days apart' between the two stickers of your Starting Double. Sometimes, you can use that 'X days apart' directly as your repeat for the sticker set. For example, the two stickers in your Starting Double may be 13 days apart, and a 13-day repeat also fits as the repeat pattern for the whole sticker set. Or sometimes, that Starting Double 'X days apart' is LONGER than what you need for your repeat pattern to be able to fit all the stickers in your sticker set onto the calendar. So then you have to find a shorter repeat interval that will still add up to (or, in mathematical terms, 'factor into') those starting 'X days apart'. How short the interval needs to be, depends on how many stickers in total in your sticker set. Usually, you will be looking at repeat intervals that are half of your starting 'X days apart', or possibly half of that again (quarters). But occasionally also thirds or fifths. FOR EXAMPLE: You may have a Calendar where the two stickers in your Starting Double are placed on 2 and 30, which is 28 days apart. That is an impossible repeat-pattern, since you cannot fit another sticker onto the Calendar with another 28 days between them (the Calendar isn't that long!) So - it has to be shorter. But how much shorter? That depends on your sticker set! Like this: In this example: If you have a Starting Double sticker set of three, then you already have two stickers on the Calendar and only have one sticker left to place. So that last one has to go in the middle of the other two stickers - to have them the same distance apart from each other. And that gives a repeat pattern of 14-day repeats for that sticker set (half of 28). With your stickers placed on 2, 16 and 30. And as you can see, 14 days between each of them. And then that same 14-day repeat pattern for all your other sticker sets too. BUT perhaps you have a Starting Double sticker set of five, so you have three more stickers to place. That doesn't work with 14-day repeats, because that would add up to much longer than your calendar! So it has to be shorter, but still an interval-repeat that will add up to 28 (or in mathematical language: that 28 is divisible by, or a multiple of). So, what is divisible into 28 ? Only 14 (which is too long for this sticker set), OR 7. Which is your solution :-) With stickers placed on 2,9,16,23 and 30. As you can see, 7 days between each of them. And then that same 7-day repeat pattern for all your other sticker sets also. REMEMBER: that the way this puzzle category is constructed, you are looking for a repeat pattern of somewhere between 5-day and 15-day repeats. Nothing larger or smaller than that. So even if your 'X days apart' can be divided by 2 or 3 or 4, those can NOT be your repeats. If you find it difficult to work out the possible repeat patterns from the 'X days apart' of your Starting Double, then take a look at the 'PATTERN TABLE' in Chapter 3. It gives all the possible repeat patterns for all Starting Double 'X days apart'. OK , enough with the text explanations - let's look at some examples... Examples: Example A - large sticker sets: See screenshot below. You have a Starting Double with 2 egg stickers on 1 and 16 = 15 days apart. A Starting Double spacing of 15 days can give only 2 possible solutions for a whole sticker set: a 15-day repeat pattern OR a 5-day repeat pattern (see *note). Here the egg sticker set has 7 stickers, and that is impossible to fit onto the Calendar if you try with 15-day repeats (the Calendar is not long enough to fit in 7 stickers at 15-day spacings!). So, it must be the shorter repeat instead. And, as easily as that, you've found your first sticker set repeat pattern: it's 5-day spacings for the stickers.

5天重复模式的解决方法： - 鸡蛋出现日期：1、6、11、16、21、26、31日 这种5天间隔的重复模式同样适用于所有贴纸套装中的贴纸。因此： - 梨子出现日期：5、10、15、20、25、30日 - 平底锅出现日期：4、9、14、19、24、29日 - 瓢虫出现日期：3、8、13、18、23、28日 - 红苍蝇出现日期：4、9、14、19、24、29日 - 黄苍蝇出现日期：4、9、14、19、24、29日 如你所见，部分日期需要贴上不同的贴纸。这是允许的。如果需要，可将它们直接叠放在一起，以将所有贴纸放入日期框中。 注意：如果难以从初始的双间隔中看出可能的解决方案，请查看第3章的模式表。 示例B - 小型贴纸套装：见下方截图。你有一个起始双贴纸，在16日和31日各有2个番茄罐头贴纸，间隔15天。并且该贴纸组总共有3个贴纸。起始双贴纸间隔15天只能为整个贴纸组提供两种可能的解决方案：15天重复模式或5天重复模式（见注）。这里你的贴纸组很小，所以重复周期必须很长，才能使组中的3个贴纸以相等的天数间隔分布在日历上。因此，它不可能是短的5天模式（那样无法在3个贴纸之间形成相等的间隔）。所以必须是较长的15天重复模式才能适用于你的贴纸组。就这样，你轻松找到了第一个贴纸组的重复模式：贴纸的间隔为15天。

解决方案 - 适用于15天重复模式： - 番茄罐头出现日：1日、16日、31日 此15天间隔的重复模式同样适用于所有贴纸套装中的贴纸。具体如下： - 黄色石头出现日：3日、18日 - 红色石头出现日：9日、24日 - 黄色叶子出现日：11日、26日 - 红绿黑石头出现日：12日、27日 - 书本出现日：13日、28日 - 灰色石头出现日：15日、30日 - 鸟类装饰品出现日：2日、17日 注意：如果难以从初始双间隔中看出可能的解决方案，请查看第3章的模式表。 示例C - 具有不同间隔的多个初始双数 查看下方截图。你有四组起始双数，它们的间隔有所不同： - 意大利面在6日和18日 = 间隔12天 - plunger在7日和31日 = 间隔24天 - 海绵在15日和27日 = 间隔12天 - 水桶在17日和29日 = 间隔12天 并且你的贴纸组大小都是2或3。 由于我们这里已经有间隔短于24天的情况，所以不可能是24天。而且，你无法在日历上以24天的间隔放置3张贴纸（日历没有那么长！） 因此，转而查看间隔为12天的起始双数。这种间隔只能为一整组贴纸提供两种可能的解决方案：6天重复模式或12天重复模式（见注）。而你这里只有3张贴纸的小组，所以重复模式必须是两种可能性中较长的那种。就这样，你找到了第一套贴纸的重复规律：贴纸的间隔时间为12天。

解决方案 - 适用于12天重复模式： - 意大利面出现日：6日、18日、30日 - plunger出现日：7日、19日、31日 - 海绵出现日：3日、15日、27日 - 水桶出现日：5日、17日、29日 此12天间隔的重复模式同样适用于所有贴纸套装中的贴纸。具体如下： - 圆盘出现日：12日、24日 - 手套出现日：9日、21日 - 电池出现日：10日、22日 - 雪花出现日：11日、23日 注意：如果难以从初始双间隔中看出可能的解决方案，请查看第3章中的模式表。 示例D - 另一个具有不同间隔的多个初始双数示例：查看下方截图。这里有三组初始双数，每组的间隔都不同： - 节拍器在第2天和第20天 = 间隔18天 - 红色U在第13天和第19天 = 间隔6天 - 黑色三角形在第14天和第26天 = 间隔12天 贴纸组的大小都是5个和6个。 你无法将5个或6个贴纸按照18天或12天的重复间隔贴到日历上（日历的长度不够！）。 而且也不可能是18天或12天的重复间隔，因为你的红色U已经有更短的6天间隔了。 对于6天的间隔，一整套贴纸只有一种可能的排列模式：6天重复。 因此，你的日历重复模式是： 所有贴纸组的贴纸均采用6天间隔。

解决方案 - 针对6天重复模式： - 节拍器标记日：2、8、14、20、26 - 红色U标记日：1、7、13、19、25、31 - 黑色三角形标记日：2、8、14、20、26 - 棋子标记日：1、7、13、19、25、31 如你所见，在此日历上，你需要在某些相同的日期贴上不同的贴纸。 示例D的另一种解法： 一种略有不同的逻辑推导重复模式的方法： - 起始间隔为18时，有两种可能的解决方案：6天重复或9天重复。 - 起始间隔为12时，有两种可能的解决方案：6天重复或12天重复。 - 起始间隔为6时，只有一种可能的解决方案：6天重复。 这里唯一的共同因素是6天重复，因此这一定是正确答案。注意：此处的示例C和D展示了，通常从间距最短的起始双贴纸开始，最容易找到贴纸组的重复模式。 注意：有些人觉得在脑中“计算”更容易，而另一些人则发现在日历上逐日计算重复次数最方便。 无论选择哪种方式，务必确保没有在任何地方数错！ 【通用提示】： 如果需要帮助从起始双贴纸间距中“看出”可能的重复模式，请查看第3章的模式表。该表显示了每种起始间距对应的可能日历模式。第三章：操作指南：详细分步说明 分步说明： （1）找到你的起始重复贴纸，并计算这两个贴纸之间相隔的天数 （2）数一下你的“起始重复贴纸组”中总共有多少张贴纸 （3）根据起始重复贴纸的间隔，找出可能的重复模式 （4）放置第一组贴纸（即起始重复贴纸组）中的所有贴纸 （5）放置剩余的贴纸组 步骤（1）：找到起始重复贴纸并计算它们之间的天数 查看你的起始日历，找到日历上初始就已放置的两个相同类型（图标完全一致）的贴纸。 日历上总会至少有一组起始重复贴纸。对于起始双贴纸——计算这两个贴纸之间的天数。 示例：一个贴纸在4日，一个在10日，间隔为6天。 提示：如果你有多个起始双贴纸，通常选择两个贴纸间隔最短的起始双贴纸会更容易找到正确答案。但无论选择哪个，你都会得到相同的结果。 步骤（2）：计算起始贴纸集中的贴纸数量：对于你的起始双贴纸——计算该贴纸集中的贴纸总数。 即：相同类型（相同图标）的贴纸总数。包括日历上已有的贴纸以及仍待放置的相同类型贴纸。 贴纸集大小通常在2到7个贴纸之间。步骤（3）：使用起始双间距找到重复模式。在步骤1中找到的起始双间距相隔的X天，决定了整个贴纸组适用的重复间距模式类型，同时也适用于日历上的所有其他贴纸组。 示例：模式表。“起始双间距”相隔X天，以及能够解决你的贴纸组和日历其余部分的可能重复模式。

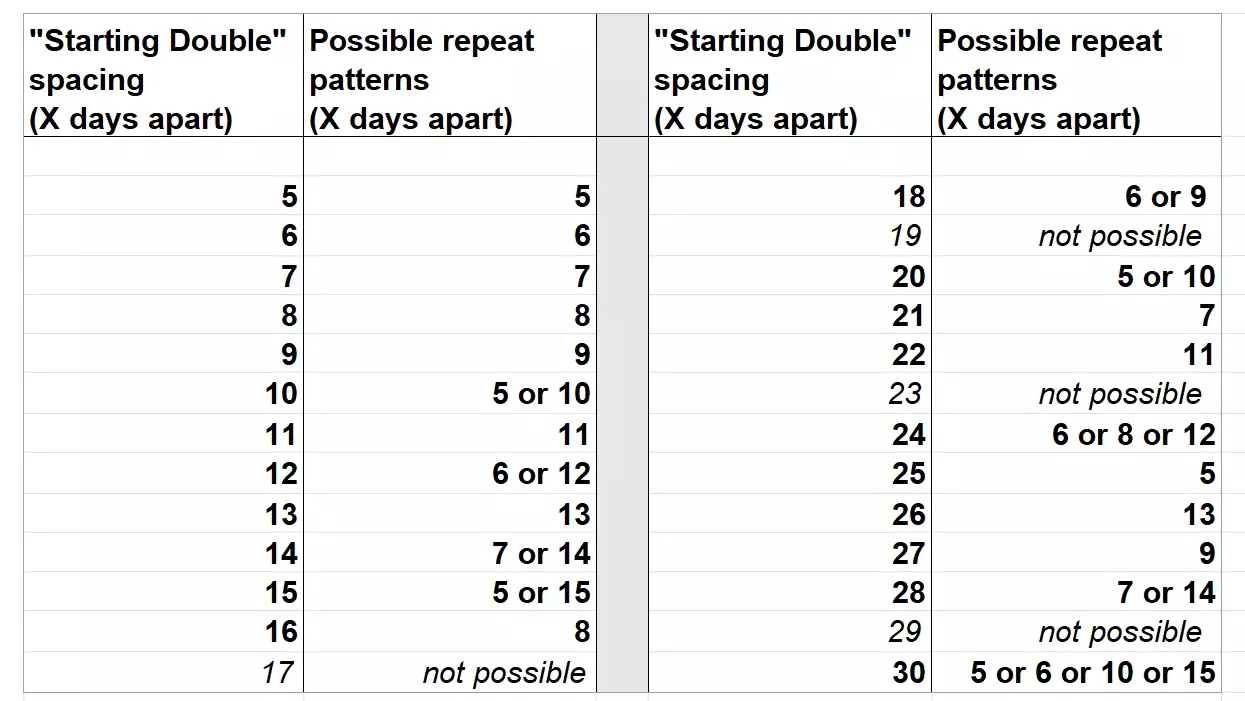
As you can see above, for many of the Starting Double 'X days apart' there is only ONE possible repeat pattern. So then you have your solution straight away. Where there is more than one possible repeat pattern to choose between for your Starting Double 'X days apart', then it's your sticker set size that decides. Small sticker sets with few stickers will need a longer repeat, big sticker sets with many stickers will need a shorter repeat. (And the exact position on the Calendar of the Starting Double can also, occassionally, make a difference.) If you're unsure which of the identified 'possible' repeats to use, just try what seems most likely. You'll quickly see which is the correct one, when you start putting down your stickers in Step (4). And note that the repeat-pattern that fits for your Starting Double sticker set, will ALSO be the same pattern for all your other sticker sets. And give you the solution for your whole Calendar. So, now you know the repeat-pattern for your sticker sets. Or what is possible, anyway. And now, on to placing down those waiting stickers....: STEP (4): PLACE all stickers in your FIRST sticker set In step 3 you found the possible repeat-pattern that will work for your Starting Double sticker set. Start counting from one of your Starting Double stickers on the Calendar. Count forwards from it in repeat intervals until you reach the end of the calendar, and then count backwards from it in repeat intervals until you reach the start of the Calendar. (Just skip over the other Starting Double sticker, when you get to it, and continue counting on in the repeat intervals.) Example: You've found (for example) a repeat pattern of 5. And on your Calendar you have, for example, a Starting Double with a heart already placed on 10 and on 25, and 4 more hearts waiting to be placed. So: count in 5-day intervals forwards from the heart already on 10: gives a heart on 15, a heart on 20, then on 25 there is a heart already, and then a heart on 30. Then count backwards from your starting heart on 10: gives a heart on 5. And that way: all 6 hearts placed, and with 5-day repeats between them (5,10,15,20,25,30) If you found a Starting Double spacing in previous section, where there were possible alternative repeat patterns, and you were unsure which would fit. Then here: try out the repeat you think is most probable, and you'll see quite quickly if you are trying with the correct one, or if you need to choose a longer or shorter repeat from the identified 'possible' ones. Find the proper repeat that fits for all the stickers in your 'Starting Double Sticker Set', before you go on to step 5. STEP (5): PLACE the REST of your STICKER SETS Use the same repeat pattern for all your other sticker sets. (The same repeat you found and used in Step 3 and 4). Example: In previous section, you found (for example) a repeat-pattern of 5. And on your Calendar you have, for example, a bird on 12, and with 5 bird stickers still to place. So: count in 5-day intervals forwards from your bird on 12: gives 17, 22 and 27. Place a bird on each of those. Then count backwards from your starting bird on 12: gives 7, and 2. Place a bird on each of those. And that way: all 6 birds placed, and with 5-day repeats between them (2,7,12,17,22,27). Repeat in the same way for each of your remaining sticker sets. Or you can use 'pattern matching' for the rest of your stickers - look at how to do that in Chapter 4 (this chapter isn't finished yet...) And REMEMBER that you can put different stickers onto the same day, if you need to. Place the stickers right on top of each other, if it's difficult to fit them all into the date box. Note that it's the centre of the sticker that defines which day it belongs to. NOTE: Some people find it easier to do the repeat counting in their heads. Other people find it easier just to count day-by-day on the calendar itself. Whatever you choose, DO make sure that you haven't miscounted anywhere! (Chapter 4: How-to : 'Pattern matching' method - not finished yet.... ) The other chapters in this Guide all describe the 'counting' method of solving the Calendar puzzles. Some of you may be more familiar with using the 'pattern matching' method for solving these puzzles: the "books 2 days after a rock, birds 1 day before a fish, ..." kind of solving. Before the Game Update, you would usually need to have placed down one complete sticker set correctly (using 'counting' method) before the rest of the stickers could be placed using the 'matching patterns' method. Although sometimes you could get Calendars where your starting stickers were placed in such a way that it could all be solved purely through pattern matching. This is still how it works now with the new Calendar variations: Mostly you will need to get your first complete sticker set placed correctly, and can then place the rest of the stickers using 'pattern matching'. (And sometimes, you may get a Calendar where the starting stickers are placed in a way that you can solve it all by pattern matching. ?? Still, or has that changed??I need to test it out...) To get your first complete sticker set placed down correctly, see the 'counting' method sections in Chapters (1-3) in the guide here. For the remaining stickers, see following examples: Example A: One starting set placed using counting method Example B: solved completely by pattern matching (EXTRA: More examples - not finished yet... ) Here are some more examples of different kinds of Calendars. Hopefully they can help you to understand better the kind of variations we can get for this puzzle category: EXAMPLE 1 EXAMPLE 2 EXAMPLE 3 EXAMPLE 4