如何将传送带分流为3路(及其数学原理)
这是一个数学证明。如果你不想阅读,可以跳过。本指南顶部有一张图片,向你展示无需数学知识的操作方法,通用使用部分还会解释如何在任意数量的传送带情况下进行操作。 图片 这是为不想看数学内容的人准备的。
警告 前方内容涉及极客知识,继续阅读需自行承担风险。 使用分数而非物品/秒来表示 我将把每条传送带的物品传输速率表示为其每秒传输物品数量与原始传送带每秒传输物品数量的比值(即分数形式)。 例如,若输入传送带每秒传输10个物品,将其分流为两条各每秒传输5个物品的传送带,那么这两条传送带的比值均为1/2。这样做是为了便于概括,避免涉及具体的每秒物品数量,从而简化计算。 从数学角度证明传送带输出为1/3 输入传送带先被分流为两条比值为1/2的传送带,接着再被分流为四条比值为1/4的传送带,其中三条1/4比值的传送带继续输送至后续建筑。第四条传送带被放回输入端,将其分割为两条1/8传送带,然后是四条1/16传送带,其中三条继续传输,依此类推。
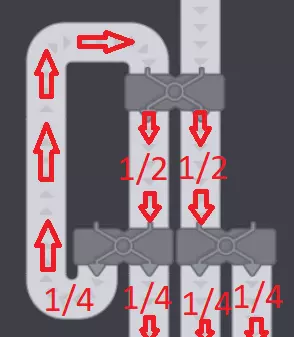
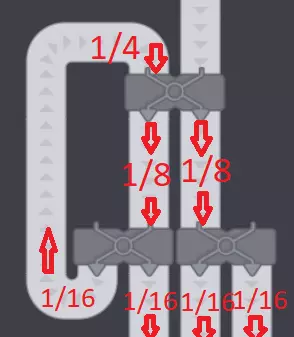
每当第四条传送带循环回来时,它就会被添加到其他三条传送带中,形成一个分数的无穷级数。 现在来进行代数运算。 设S为添加到一条输出传送带的无穷分数之和。 S = 1/4 + 1/16 + 1/64 +... 第一步是将等式两边同时乘以4: 4S = 4×(1/4 + 1/16 + 1/64 +...) 根据分配律,括号内的每一项都乘以4: 4S = 1 + 1/4 + 1/16 + 1/64 +... 下一步是将等式两边同时减去1: 4S - 1 = 1/4 + 1/16 + 1/64 +... 这一步用S替换无穷级数,因为等式右边与S的定义完全相同: 4S - 1 = S 最后一步是求解S: 4S - 1 = S 两边同时减去4S: -1 = -3S 两边同时乘以-1/3: -(-1/3) = -(-3S/3) 1/3 = S 即1/3 = 1/4 + 1/16 + 1/64 +...为什么简单方案不可行 简单方案看似显而易见:“为什么不直接不用其中一个输出口呢?既然有3条传送带,忽略一条不就行了。”但问题在于,分配器(splitter)如果没有两条传送带可供分配,就无法对传送带进行分流,因此它会将所有物品都输出到一条传送带上,而不是两条。这样一来,最终会产生两条1/4负载的传送带和一条1/2负载的传送带,而不是三条各1/3负载的传送带。

采用这种配置,部分建筑会接收过多物品,而另一些则接收不足。效率是游戏的关键,不能让如此简单的问题导致严重的效率低下。 更通用的用法: 同样的逻辑可用于将一条传送带均匀分流为任意数量的传送带。你只需找到一个最小的数字,将其乘以几次2后等于你想要的传送带数量(一个简单的方法是:取你想要的传送带数量,不断除以2,直到无法整除为止),然后将传送带分流为下一个最大的2的幂数(2、4、8、16、32等),将多余的传送带送回输入端,再对剩余的传送带进行分流,直到得到你想要的传送带数量。更通用的用法(示例) 在此示例中,我将把一条传送带分成10个相等的部分。 首先将10除以2,直到无法整除。 10/2=5 然后将传送带分成下一个最小的2的幂,即8个部分,并将多余的3个部分送回输入端。
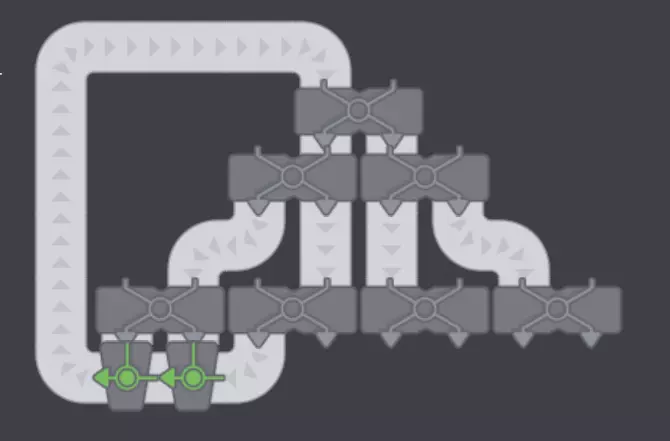
然后将剩余的5条传送带均分成两半
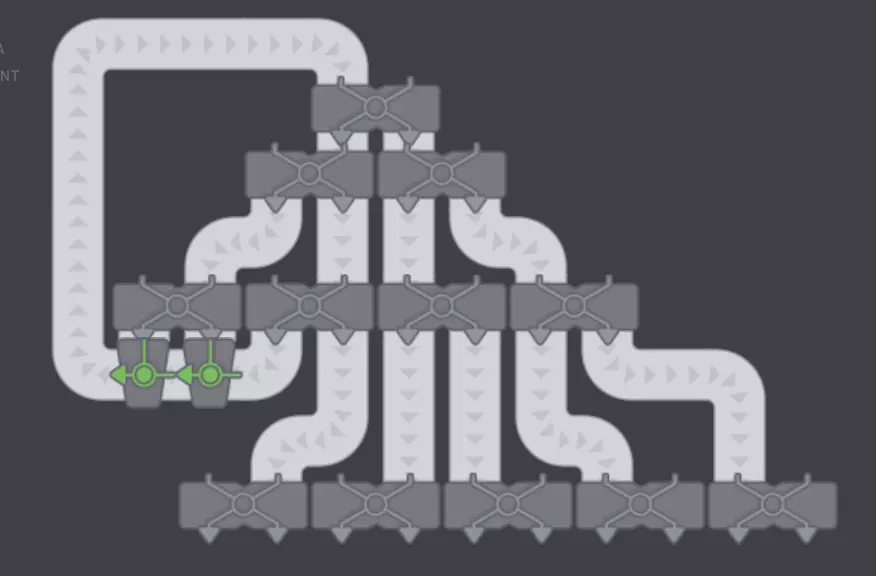
然后将输出发送到你想要的任何地方。 我记得有分流器和合流器。 我将快速演示如何使用分流器和合流器进行设置,这样会简单得多,也不需要太多思考。 首先,创建一排输出接口。 其次,为每隔一个输出接口添加一个分流器。
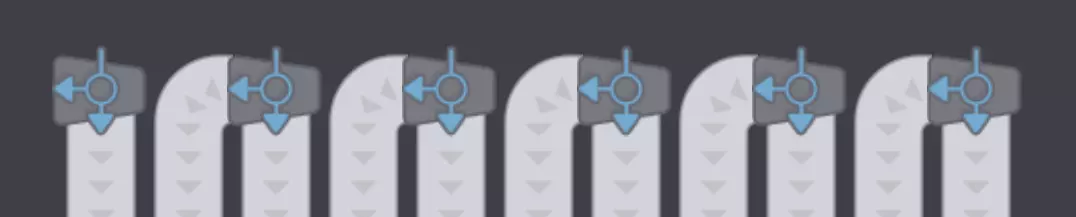
第三次重复步骤2,直到只剩下2个分流器
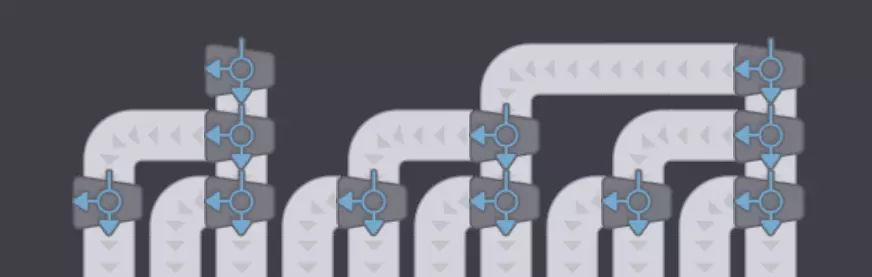
第四次重新连接未使用的输出接口。
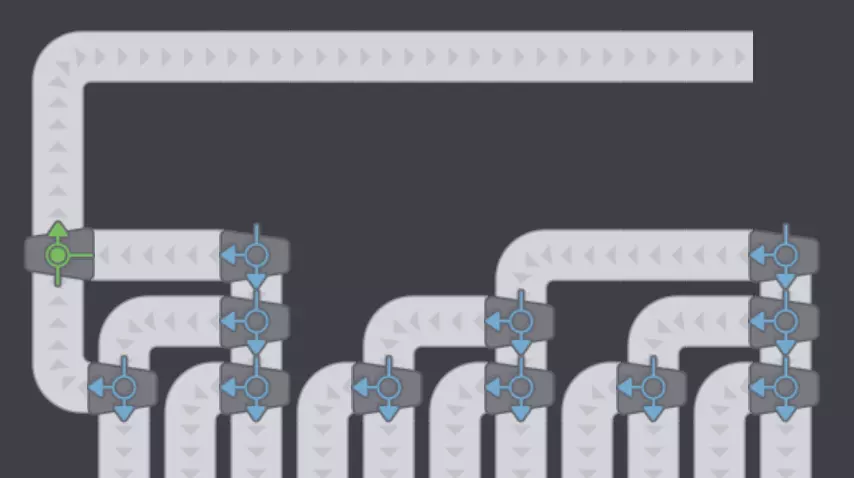
第五步,使用平衡器重新接入未使用的输出和输入。
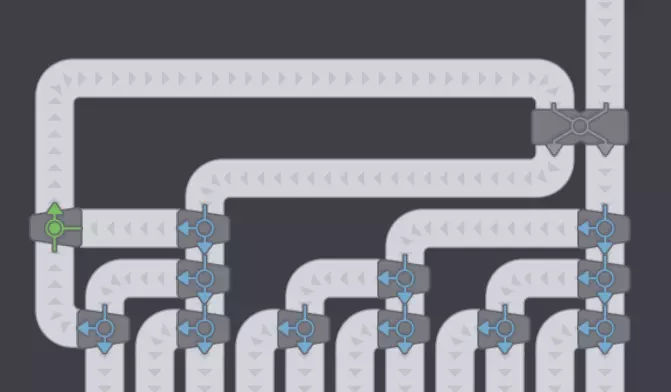
如果在此步骤中使用分流器和合流器而非平衡器,分流器与 inserter(机械臂)之间的传送带上的物品/秒将超过最大值,从而导致堵塞并降低效率。
就这样。 特别感谢 本指南的灵感来源于另一篇指南下的一条评论,该评论提出了简单的方案,同时也源于我对数学和过度思考自动化游戏的热爱。 感谢您阅读我的第一篇指南,如果我犯了错误请告诉我。我是在凌晨2点写的这篇指南,后来发现自己对它深恶痛绝,所以我不会接受任何反馈,并会立即完全忘记这篇指南,因为现在已经凌晨3点了,而且我也没有好好校对。好吧,这次是认真的,我不会再回来了。我只是必须加上关于分流器和合流器的那部分内容。 n个输出的一般证明 我带着新知识和一块白板回来了。这是一个通用证明,如果你愿意解读我的潦草字迹的话。 一般证明

n=5的情况
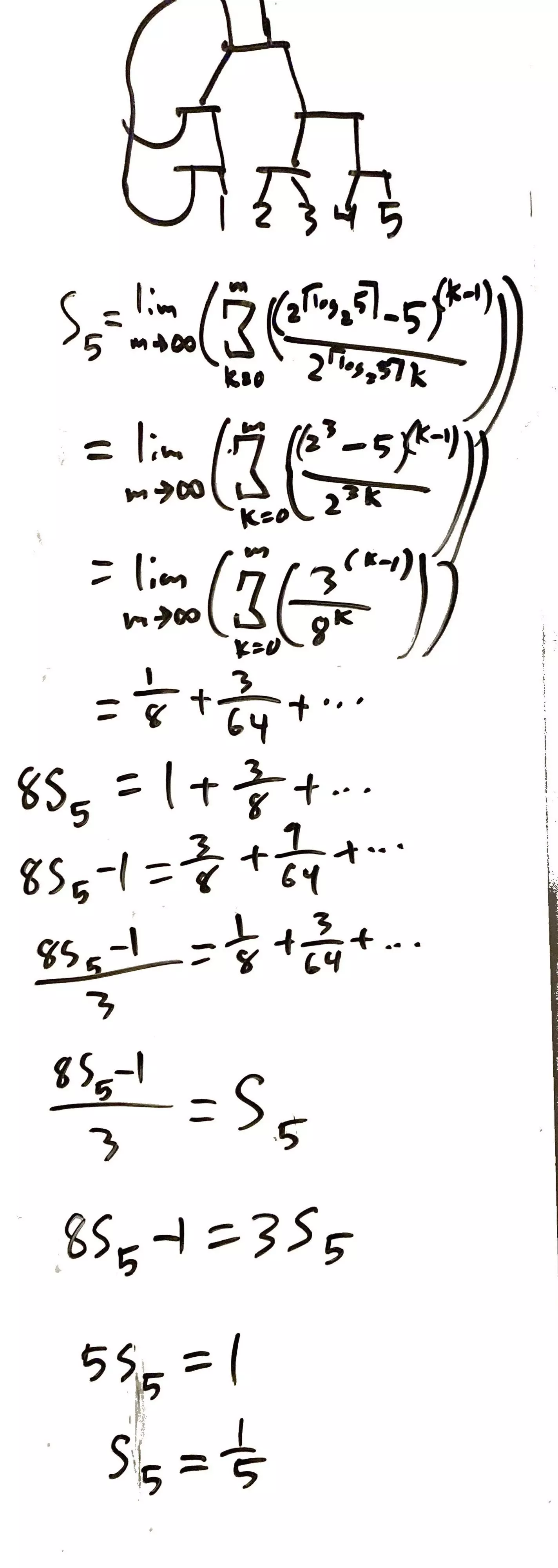
如何将传送带分流为3路(及其数学原理)
2026-02-16 04:00:26 发布在  异形工厂(Shapez)
异形工厂(Shapez)
说点好听的...
收藏
0
0