我原以为10×10的网格是最佳选择，但事实并非如此。 （2022年10月6日小更新，增加了关于中型道路的更多内容。） 简介

我一直觉得，如果要建一个规整的正方形网格，那肯定得是10×10的：这样每个区块都能完全分区，道路长度高亮和道路引导圈也让绘制变得简单。 但事实证明，我们可以做得更好。 你能猜到什么尺寸最好吗？你能证明吗？ （作者：me22ca） 数学时间 对于10×10的网格，计算很简单：在10²的区域内，我们能得到8²的可分区格，密度正好是64%。（这里以及本节其余部分，我们假设使用小型道路，即2单位宽的道路。） 对于边长为n的正方形的一般情况，可分区面积为(n-2)² - max(0, n-10)²——即道路内部的面积减去中间无法到达分区的区域面积——而总面积为n²。我很难在脑子里理解那个商数，所以我们还是把它画成图表看看会怎么样吧。

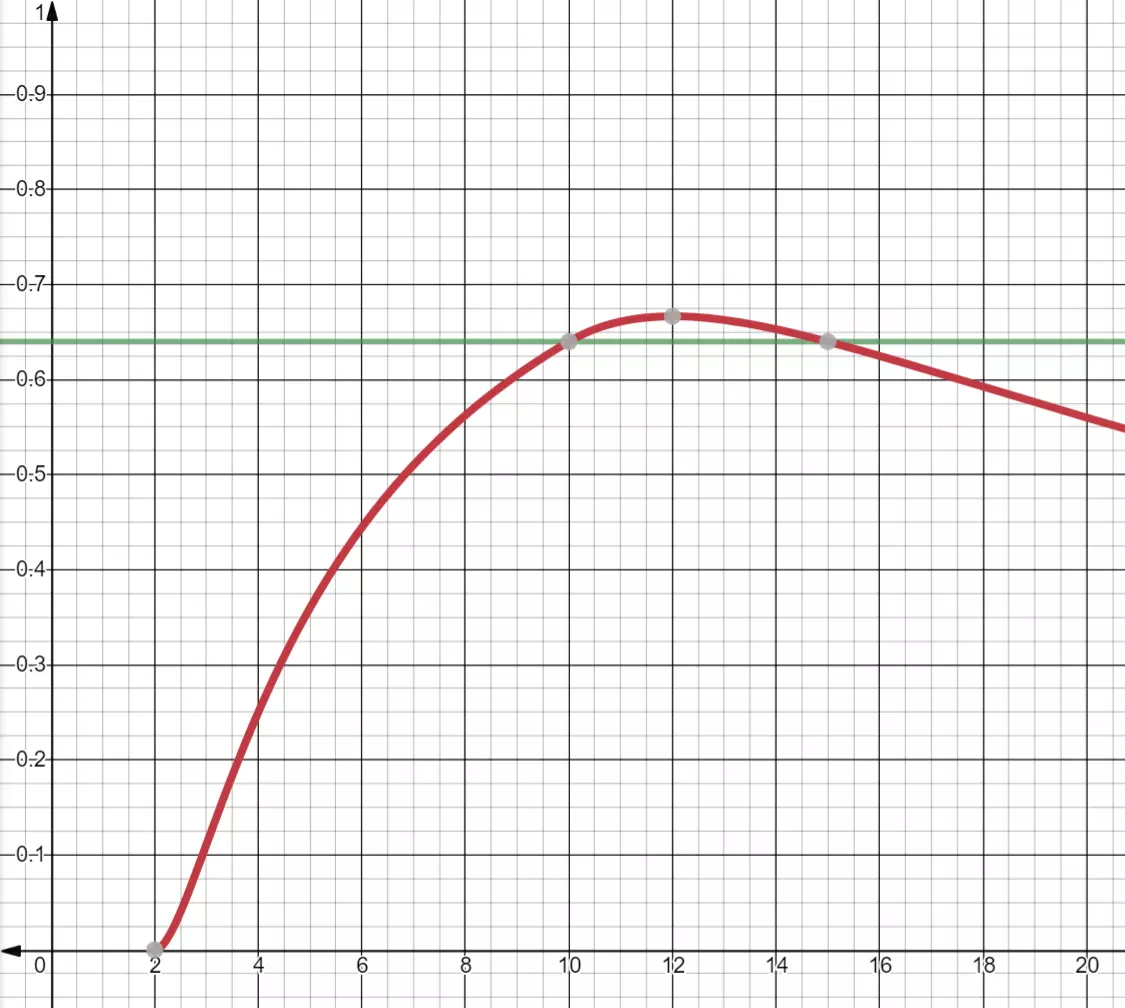
这表明“显而易见的”10×10网格实际上与15×15网格效果相当。

看起来12u是最佳选择。我们能证明吗？当然可以，让我们回到微积分I： 0 = d/d [(-2)² - (-10)²]/² 0 = d/d [(-2) + (-10)]×[(-2) - (-10)]/² 0 = d/d (2 - 12)×8/² 0 = d/d (16 - 96)/² 0 = [(16)ײ - (16 - 96)×2]/⁴ 0 = (16 - 32 + 192)/³ 0 = -16 + 192 = 192/16 = 12 因此，没错，正是12的块长度能提供最佳密度。

（巧合的是，这也是《城市：天际线》中轴对齐道路的最大路段长度。） 改进了多少呢？区域面积占比从64%提升到了三分之二（66.66…%）。 我承认，仅多4%左右的可分区面积听起来可能没那么令人兴奋。但这不仅密度更高，而且成本更低。 为什么呢？因为你需要为道路付费。对于10×10的街区，64格可分区面积需要40单位的道路（1.6格/单位），而12×12的街区仅用48单位的道路就能获得96格可分区面积（2格/单位）。因此，在相同区域内规划更多建筑时，道路支出减少了16%。下面用具体数据进行对比：以60×60的区域（便于多种方式均匀划分）为例，使用不同的区块尺寸和基础小型双车道道路，数据如下： 区块长度（单位） 可规划区域（平方单位） 道路长度（单位） 道路成本（₡） 道路维护费用（₡/周） 6 1600 1200 48,000 384.00 10 2304 720 28,800 230.40 12 2400 600 24,000 192.00 15 2304 480 19,200 153.60 20 2016 360 14,400 115.20 30 1536 240 9,600 76.80 因此，如果你采用10×10的网格，为获得相同的区域面积，你将多花费50%的成本。 （该表格还显示，可规划区域的下降速度慢于道路成本，但不要忘记，对于任何有影响半径的服务设施，较低的密度也意味着更高的成本。） 结论：如果你想要最密集的方形网格，请采用12×12的尺寸（使用小型道路）。与10×10网格相比，在相同空间内可多容纳1/24的 RICO建筑，同时道路支出减少1/6。

附录A：中型或大型道路

如果你使用的是4单位宽的道路，比如中型道路和大型道路，那么最佳密度的方形网格是16×16。但使用较宽的道路会让你付出沉重的密度代价：只有50%的区域可用于分区规划。（你可以通过4×4的区块来直观计算：在16×16的空间中总共有16个区块，其中8个可分区，1个在中间空置，7个是道路。）需要强调的是，50%的密度与使用小型道路的24×24网格相同。在使用2单位道路的方形网格中间留下一个巨大的14×14不可分区空洞，其密度竟然与使用4单位道路的最佳情况相当。因此，如果你发现自己希望网格中有更多车道，考虑使用成对的2单位单向道路，而不是换成4单位道路。获得额外的临街面会带来很大不同。例如，如果你在脑海中将16×16网格中的双向四车道中型道路“一分为二”，最终会得到8×8网格的单向双车道小型道路。这不是一个特别高效的网格，但它的密度仍然比使用中型道路的网格高出12.5%（9/16比1/2），而且还有一个好处是可以避免出现交通信号灯，获得更多停车位，并且减少交叉口的冲突点（单个完整的四向双向交叉口有32个冲突点，而四个四向单向交叉口每个只有5个——减少了37.5%）。 为了完整起见，如果你使用创意工坊中的6u（48米）超宽道路，使用20×20网格时的最佳分区密度为40%。但这些通常是工业道路，主要用于工业DLC建筑或其他可放置建筑，而非分区RICO建筑，因此此计算并不相关。 附录B：矩形区域 矩形区域越长，其密度可以任意接近80%的上限†。 对于α×β大小的街区，密度公式为((α-2)(β-2)-(α-10)(β-10))/(αβ)=8(α+β-12)/(αβ)。为简化计算，假设矩形的两边均为10或更长（显然，如果两边都小于10，密度会比正方形更低，而像5×50这样不合理的街区不在讨论范围内）。 因此，如果你想获得比10×10街区更好的密度，其实有不少选择。

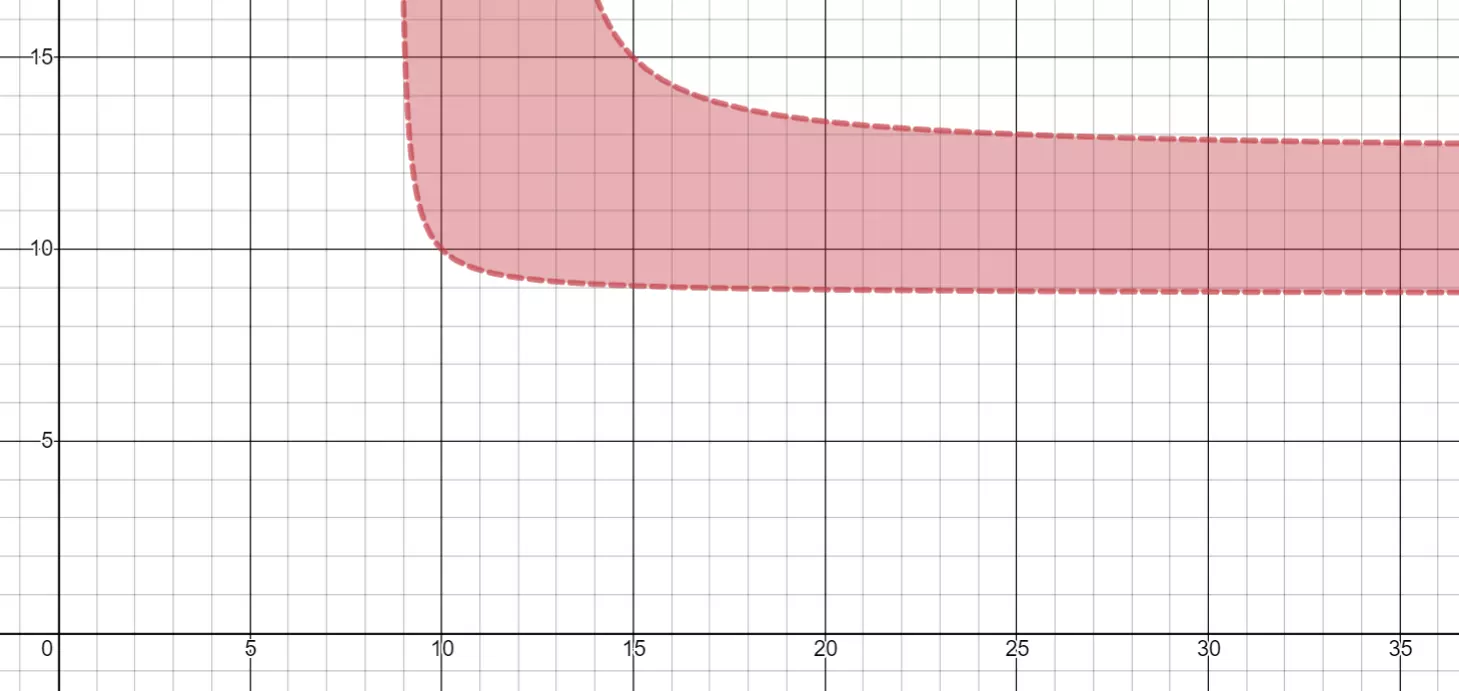
但如果你想击败12×12的方块，你的选择会受到更多限制。

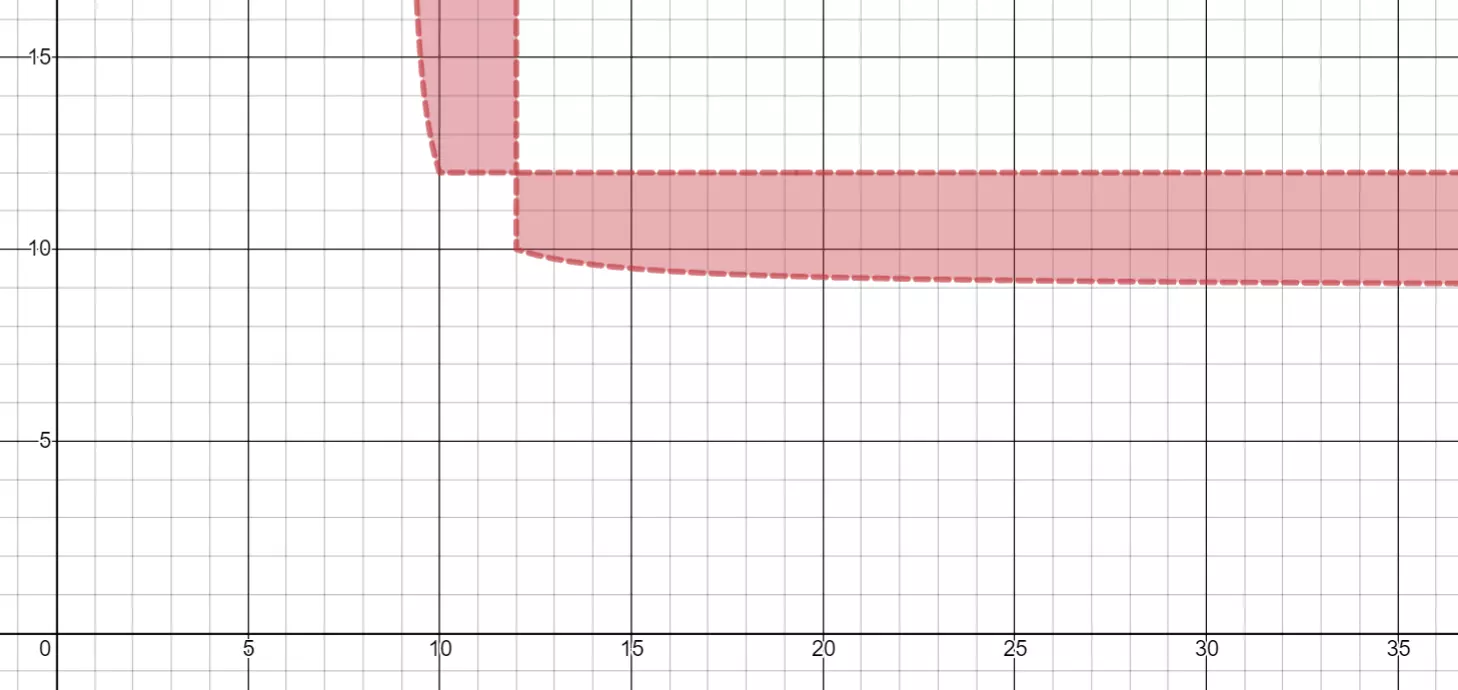
有趣的是，这也表明对于更大尺寸的区块，12乘以任何数都能达到12×12区块的效果。仔细想想，这其实是合理的：中间的横截面宽度为12单位，分区为8单位——占整体的三分之二，所以你可以随意增加更多这样的部分，而不会改变整体密度。或者，将β=12代入公式并简化也能证明这一点：β-12这部分会消失，只剩下(8α)/(α×12)=三分之二，因为α≠0。 实际上，如果你将自己限制在整数范围内（这样你就可以使用【按道路长度对齐】功能来绘制），那么唯一能胜过最佳正方形区块的是α属于{10,11}，β属于{13,14,15,...}。 好多少呢？10×16的密度为70%，比12×12正方形区块高出5%。要达到75%的密度需要10×32的布局，这种布局比我个人喜欢的网格更呈长方形，但如果你习惯了纽约的布局，可能会有不同看法。 不过这一切都有些不尽如人意，因为渐近线意味着我们无法做出最佳的布局。相反，既然我们不希望区块太窄，不如尝试通过设定特定的宽高比≥1来重新参数化，令β=α。 当α=24/(+1)≥10时，密度达到最大值。作为合理性检验，对于正方形（=1），这正确地得出了我们之前找到的α=12。但该式的定义域限制相当严格；即使=2，也得出α=8，因此并不适用。这意味着对于较大的，我们又回到了10×10的布局，这同样说明不了太多问题。但这个临界点在哪里呢？当α=10时，解得=14/10，由此得到一个便于计算的10×14的区块大小，其密度为24/35≈68.57%。

所以，从某种意义上来说，这或许是“最佳”的网格布局，因为它是在不会让最佳区块在中间留下分区空隙的前提下，能使用的最接近正方形的宽高比。 额外的密度是否值得以牺牲规整性为代价？这个问题我留给你来判断。 † 限制条件是平行线无限长且永不相连，这样就不会有任何潜在可分区的区域被横向街道占用。快速查看此类道路的横截面会发现，每侧有4单位可分区空间，道路本身为2单位，因此密度为(4+4)/(4+2+4)=0.8。附录C：真实城市 网格尺寸（链） 城市：天际线尺寸（u） 提姆加德（罗马） 1⅓ 3⅓ 波特兰 4 10 休斯顿 5 12½ 危地马拉安提瓜 5½ 13¾ 明尼阿波利斯 6¼ 15½ 渥太华 4×9¼ 10×23 纽约 4×14 10×30 费城 6¾×8½ 17×21 克赖斯特彻奇（市中心） 6×12 15×30 盐湖城 12 30 这些数据通过卫星地图测量得出，包含道路宽度（不仅仅是临街长度），因此可能与其他地方的“标准”答案不完全一致。例如，波特兰交通局表示其街区长度为200英尺（≈7.6u）。 【网格尺寸（间‡）】【近似城市：天际线尺寸（u）】 大阪（船场） 50 11 京都 38×76 8½×17 名古屋 60 13½ 感谢评论区用户@eightroomofelixir建议增加更多日本城市——我最初只收录了名古屋。（注意：日本表格仍在完善中，因为我在单位换算方面遇到了一些不确定因素，希望确保数据的准确性。） ‡参见日本长度单位相关内容。 为什么用测链？ 因为这些网格大多有100-300年的历史。测链单位是17世纪英国天文学家埃德蒙·冈特的发明。它的长度为66英尺，即1/80英里（约20.117米）。 在美洲的英语殖民地，土地边界是用测链单位来测量的，这是计算英亩面积最方便的单位。1英亩等于10平方测链。 ~ 出自洛拉·卡齐尔所著《公共领域的测量与测量员》以澳大利亚为例，该单元还解释了以下看似奇怪的长度规定： 我最初规划主街宽度为九十九英尺，规划完成后，总督却下令将其改为六十六英尺。但在我向总督极力劝说并使其相信宽阔的街道有利于健康，且对未来的维多利亚市而言更为便利后，他同意了我的方案。因此，我不再反对三十三英尺宽的窄巷规划。 ——罗伯特·霍德尔，1837年虽然我通常会使用米作为单位，并且实际上在卫星地图上也是以米为单位进行测量的，但或许更准确的说法是（例如）波特兰的网格为4链（因此每英里20链），而不是直接写出我得到的各种测量结果。尤其是因为可能存在1链宽的道路和3链的临街面：3链等于198英尺，这可能比他们网站上所说的200英尺更准确。 † 当然，作为一种古老的英制单位，链的长度因地区而异。如今你可能会认为它是12573/625米，但实际上在美国是79200/3937米，在英国则是4400000/218723米。想深入了解这百万分之二的细微差别吗？附录D：异构道路

bindulanija在评论中询问了混合使用小型道路和中型道路的问题。 结果发现，无论是每个方向选择一种尺寸（例如横向使用小型道路，纵向使用中型道路），还是在两个方向交替使用道路（比如叠加两个尺寸为两倍、相互偏移的网格），都没有影响，因为((-2)*(-4)-(-10)*(-12)) = ((-3)*(-3)-(-11)*(-11)) = 16(-7)。 因此，当混合使用2u和4u道路时，14u的网格是最优的，密度为4/7≈57%。 个人建议采用交替道路策略，以避免在任一方向上偏向交通容量。