希望你正在阅读游戏海报，我将为你介绍《坎巴拉太空计划》宇宙中的物理特性和基本原理。我是一名物理学家，接下来会探讨游戏宇宙中的动力学、运动学、航天器、力学以及火箭相关主题。放心，这不是物理课程，我也不会收费。我会在有时间时更新缺失的部分。 动力学与运动学 首先，动力学是物理学的一个分支，研究作用于运动物体上的力以及物体在这些力的方向上的运动。这些问题可以更详细地研究，而我将仅通过物理定律和实例来分析游戏宇宙的建模方式。 我会从三个部分来探讨游戏的动力学。行星与小行星的动态，物体的动态以及火箭的动态。 行星与小行星的动态

我会将游戏中的太阳系命名为“坎星系”，因为其中恒星的名字是“坎星”。坎星系中有1颗恒星和6颗行星。为了不让本指南变成物理课，我不会去解复杂的方程组，而是会将其与我们自己的太阳系进行对比，以便于理解。 游戏中我们的母星“坎星”的重力加速度与地球的重力加速度之比为1.08。从这一点来看，我们可以用已知的物理定律来理解坎星的动力学。

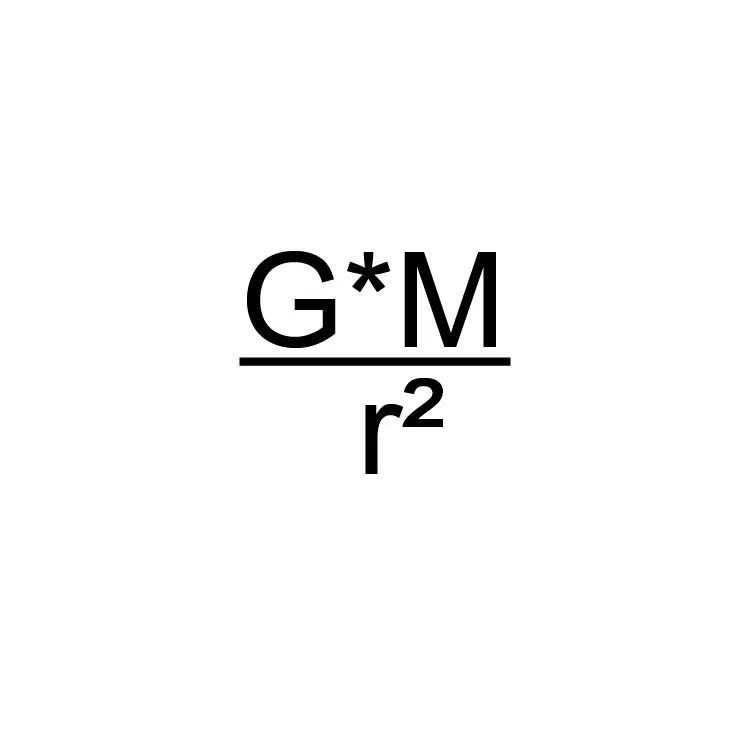
如果我们将已知的关于坎巴拉的信息代入上述方程，计算得出的坎巴拉重力加速度为9.807米/秒²。给定值与计算结果之间存在1.0003的差异。根据此计算，误差 margin 为0.03%。对于这款游戏而言，如此小的数值可以忽略不计。 我们可以将此结果理解为该星球上的物理运动是按照真实物理定律建模的。让我们也来研究一下坎巴拉在太空中的运动。为此，我们将使用以下方程。

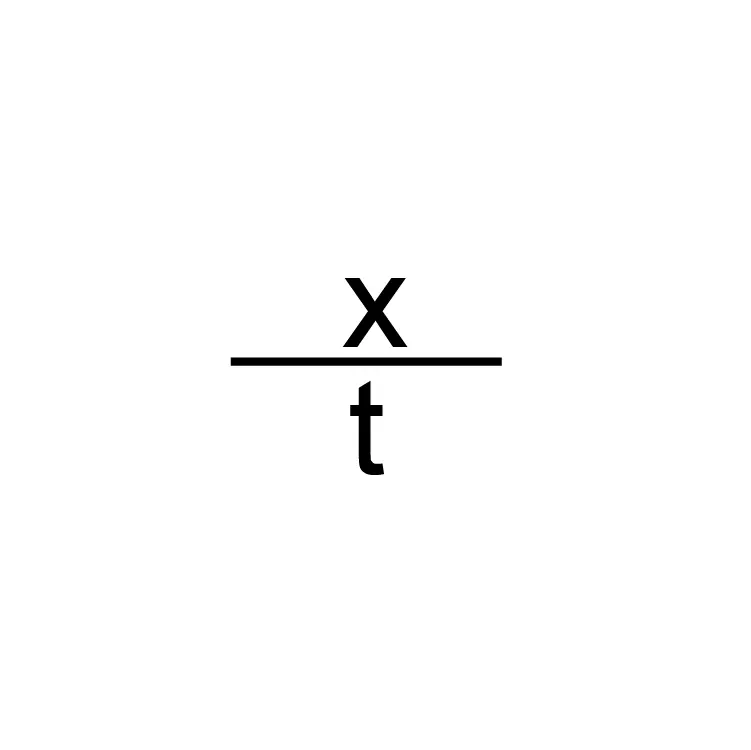
再次，以地球的相关信息作为参考，我们可以得出，根据真实物理定律，坎巴拉星球给定的轨道速度存在0.01%的误差。同样，由于这个数值很小，我们可以认为游戏中行星在太空中的运动是按照真实物理定律建模的。 天体动力学 我们可以更详细地研究行星和太空中不同情况下的天体动力学。我们将测试一般情况及其与真实物理定律的符合性。我们将使用下面的受力分析图来进行这项工作。

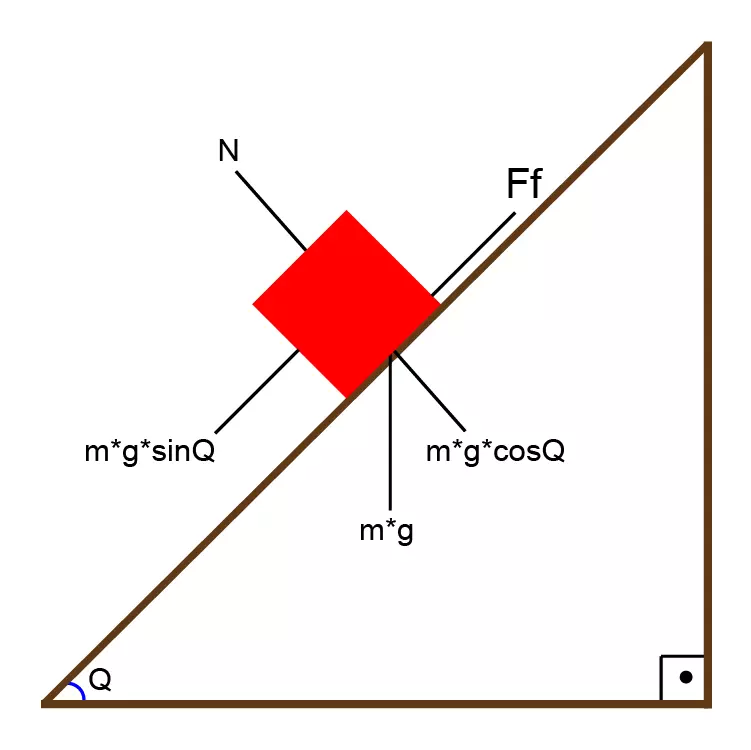
为了测试这一点，我选择了【Kerbin】星球，运用上一主题中计算出的结果，并创建了以下实验装置。在该实验装置中，我将一个质量为1346千克的物体从972米高度无初速释放，它在14秒后到达地面。如果我们将这个实验与上述方程结合来理解其实验装置，就能得到这样的结果。

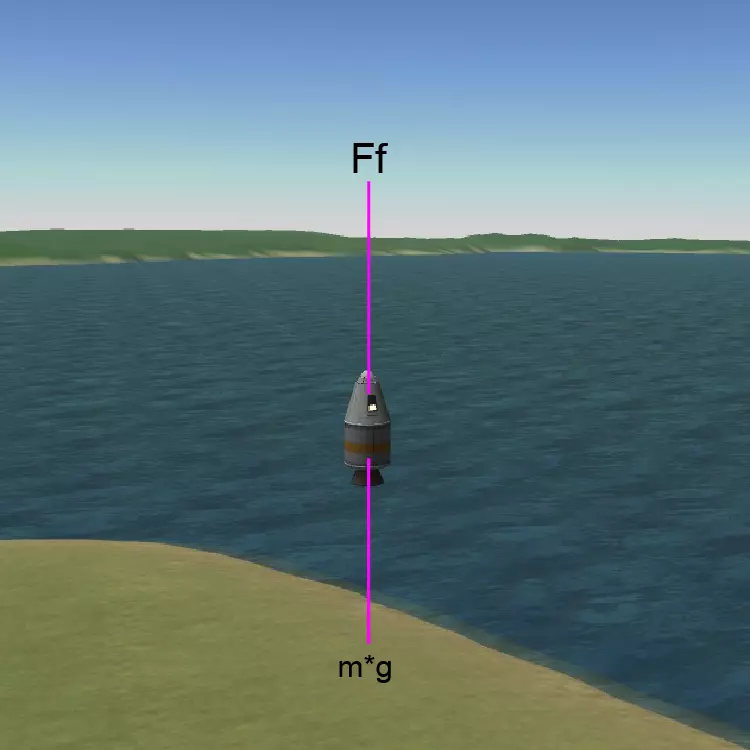
如果我们使用以下力学方程来测试我们在本实验中获得的真实物理定律。

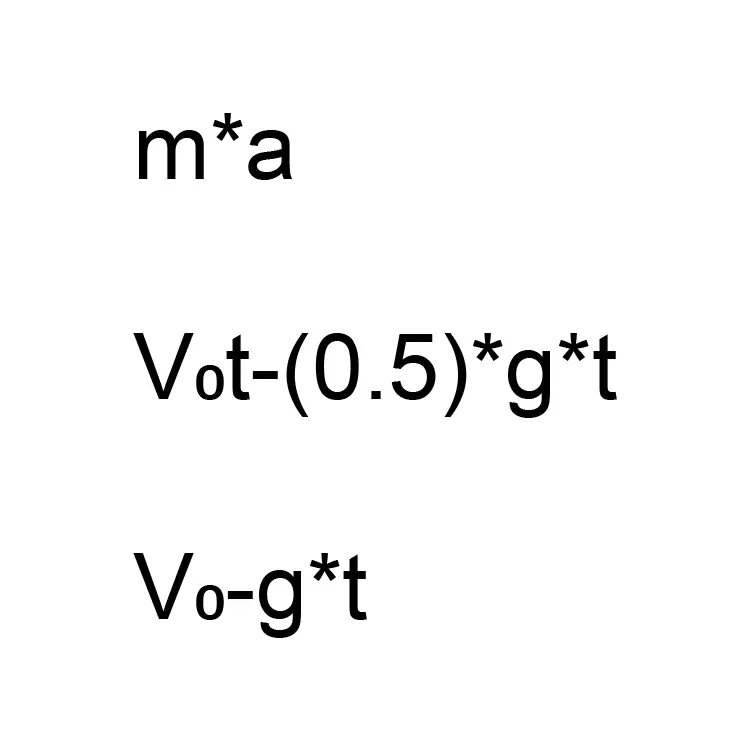
我们可以通过力学公式、实验结果以及实验中的信息来证明计算的准确性。因此，我们可以说游戏中的物体动力学也是根据真实物理定律建模的。 我想测试的最后一个属性是空气密度。通过这种方式，我们将分析完一颗行星的所有必要信息。为了进行测试，我选择了【Kerbin】行星，利用我们在上一主题中计算出的结果，并创建了以下实验装置。在该实验装置中，我在514米高度完全打开mk16降落伞，重量为1146千克的物体以6.2米/秒的平均速度在118秒内到达地面。如果我们将这个实验与上述方程结合起来理解其实验装置，就会得到这样的结果。

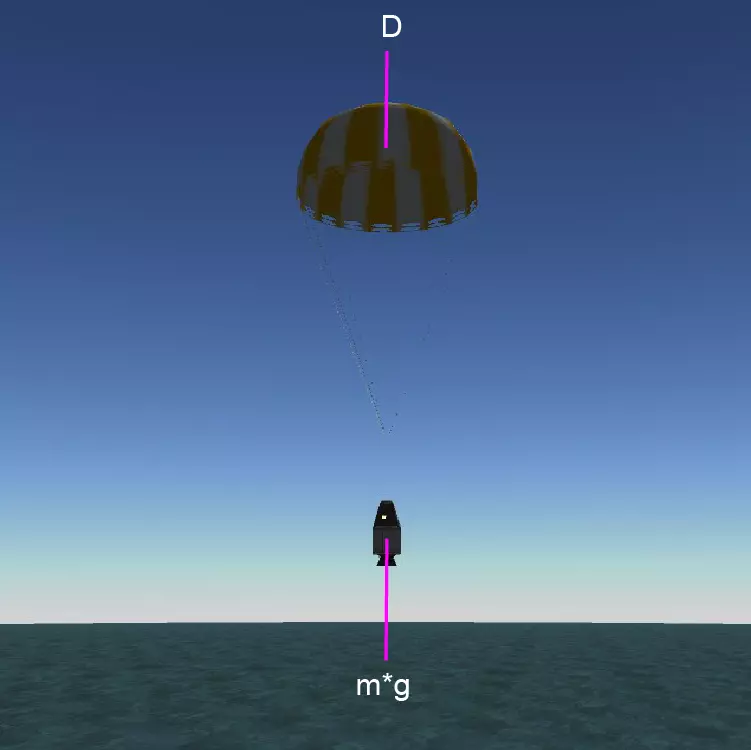
在本实验中，为确保结果的准确性，我使用了Rocket Fx程序。我将实验中的信息输入该程序，并将本次实验与所提供的信息进行了对比。依据真实的物理公式，我计算出该实验的误差率为0.58%。

你可以在Rocket Fx上找到更多相关详细信息。根据这个结果，我计算出Kerbin海平面的空气密度为1.21-1.22 kg/m³。根据所提供的信息，Kerbin的大气层仿照地球的美国标准大气（USSA）设计，但垂直高度比例缩小了20%。你可以在游戏的维基网站上找到关于Kerbin大气密度的更多详细信息。 航天器物理 这是学院讲座的主题。因此，我将把航天器物理分解成几个部分，并分析《坎巴拉太空计划》游戏动力学中的一些要点。 航天器动力学：真空和大气层中 实际上，航天器是简单的结构。它们唯一的用途就是成为能够在太空中航行的载具。我们可以以阿波罗11号或特斯拉Roadster为例。这两个例子中的航天器都是遵循相同的物理定律被发射到太空中的某个地方。一个瞄准的是一个点，而另一个瞄准的是一条轨道。我会在另一个主题中把轨道部分作为轨道力学来分析。现在让我们看看能否利用真实的物理定律，在《坎巴拉太空计划》中把一艘航天器送到另一块太空岩石，就像阿波罗11号瞄准月球那样。这次我会在实验前先进行理论分析工作。 如果你在大气层中以某个角度投掷任何物体，我们可以用以下公式计算出达到一定射程所需的功率。

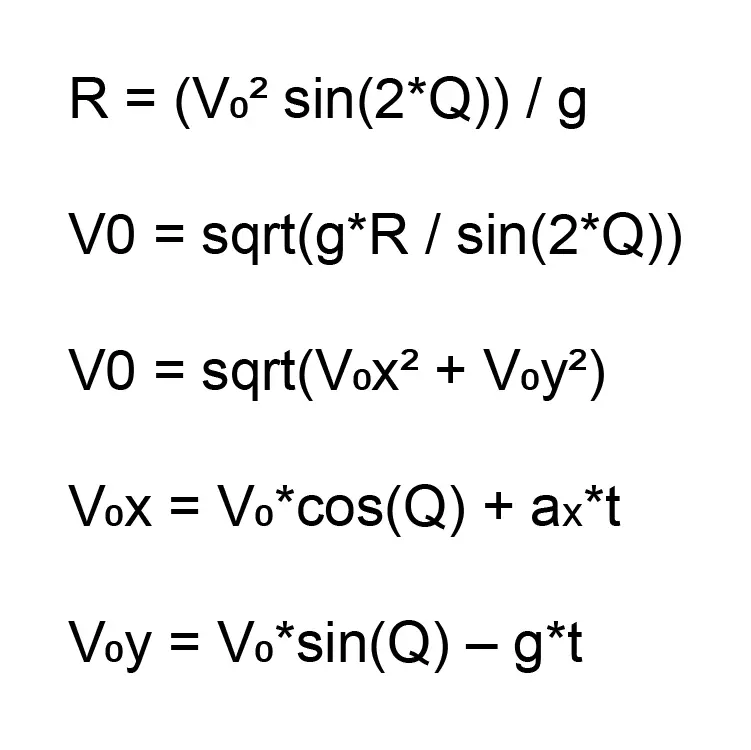
经过此计算后，我们可以使用以下公式来计算所需的力。

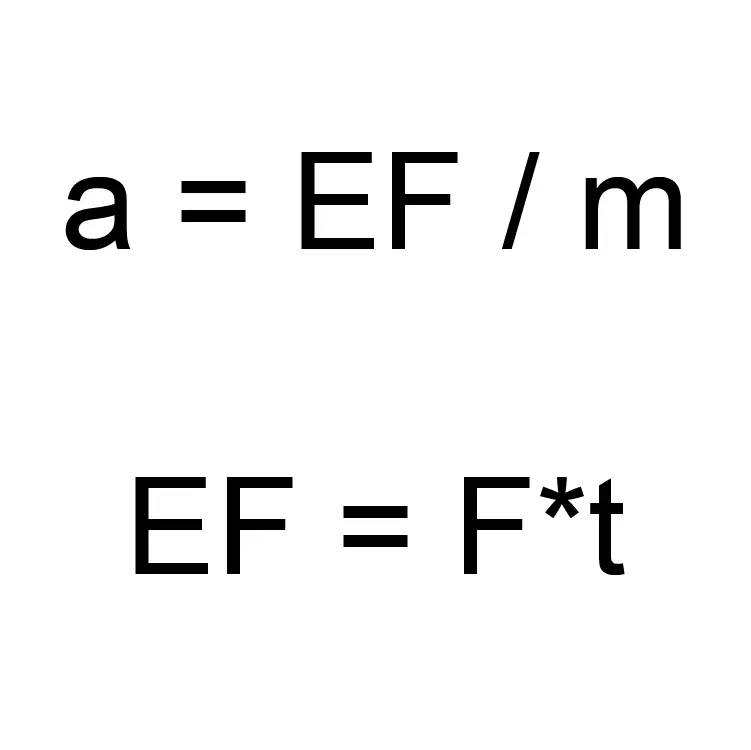
为了研究航天器在太空中飞行的这些公式，我们必须从动力学转向航天动力学。为此，我们还需要进行两项计算，即稳定性和Delta V（德尔塔V）。我将使用Rocket Fx应用程序中的推重比页面来计算稳定性。我会根据《坎巴拉太空计划》维基上发布的Delta V地图来分析Delta V参数。

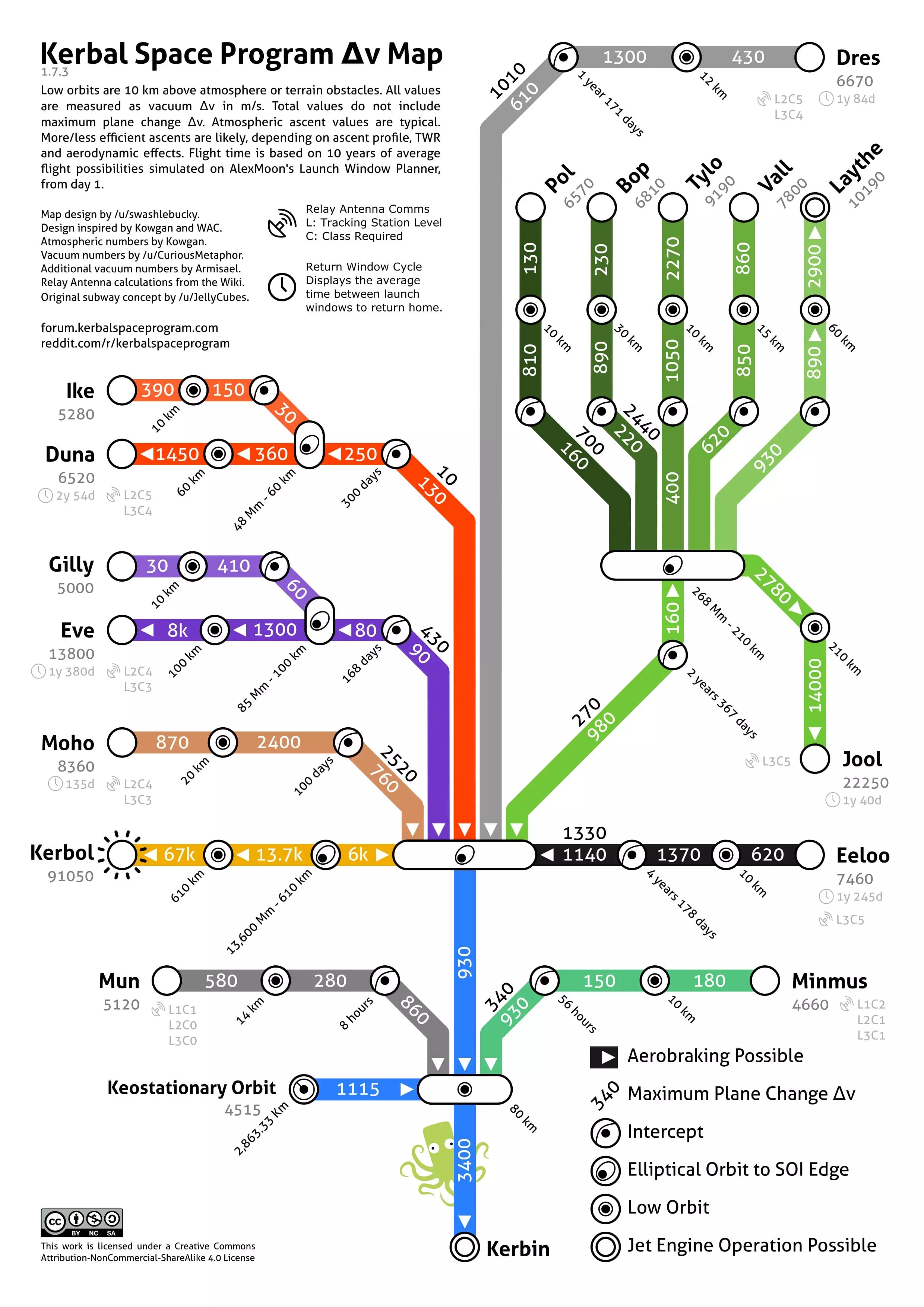
根据地图显示，我们需要3400米/秒的ΔV才能进入80千米高的近坎星轨道。为了让分析更清晰，我会尝试用一枚简单的火箭，以3400米/秒的ΔV进入平均高度75千米的近坎星轨道。我也会在这类计算中考虑灵活性余量。 首先，我会重新进行计算。如果我们尝试用真实物理公式计算从坎星表面进入近坎星轨道所需的3400米/秒ΔV数值，就需要使用以下公式。

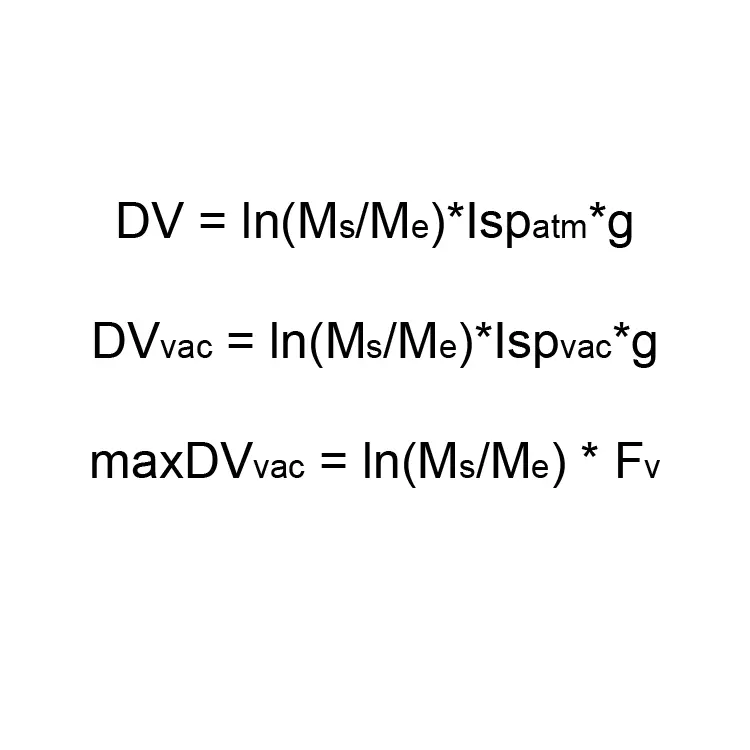
因此，对于总DV，需要使用上述结果在下方公式中重新计算。

既然理论已经准备就绪，我可以利用《坎巴拉太空计划》中的信息来建造一枚火箭，并分析结果是否与理论相符，即《坎巴拉太空计划》中的航天器是否按照真实物理规律运行。 我将为火箭配备一个座舱，在座舱上安装一个整流罩以减少气动效应，还会配备燃料箱和发动机。

根据上述计算，我设计的火箭的Δv为2833.9米/秒，而《坎巴拉太空计划》计算的Δv为2831米/秒。根据Δv地图，我计算出在真空中3400米/秒的Δv实际需要3554米/秒的真空中Δv，才能进入约73.5千米的圆形轨道，且火箭仍剩余77米/秒的Δv。实际上，我进入该轨道使用了3477米/秒的Δv。这使得《坎巴拉太空计划》的Δv计算误差 margin 为0.1%。根据Δv地图得出的轨迹和Δv差异可能因火箭的上升剖面而异。不过，对于《坎巴拉太空计划》而言，若有优秀的飞行员和更佳的上升剖面，出现8.8%误差的轨道且误差 margin 为2%的情况是可以排除的。

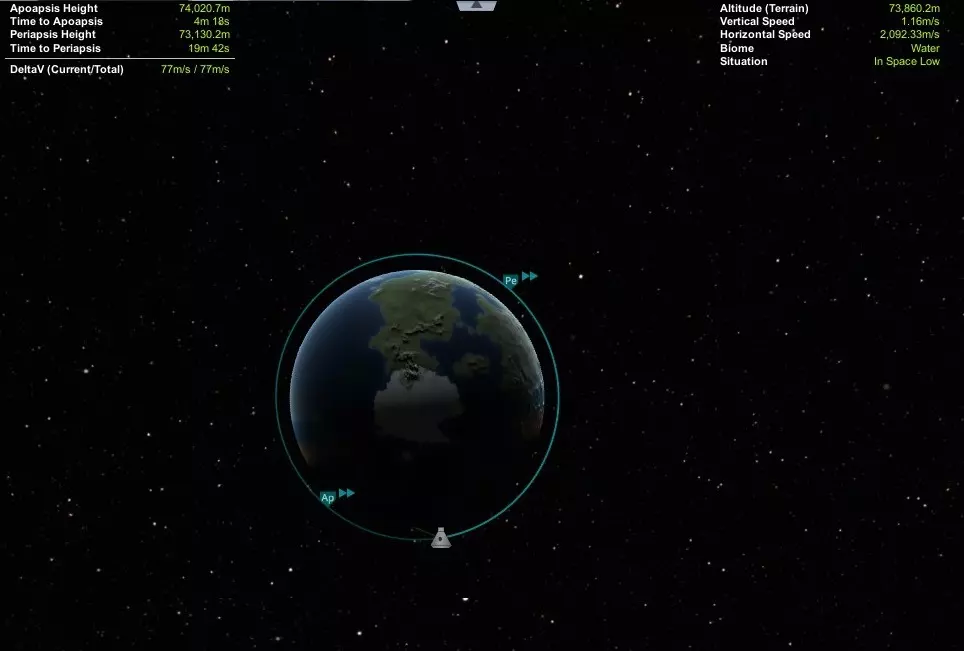
影响火箭高度的最大因素之一是火箭的稳定性。通过计算推重比可以了解其稳定性。因此，我将使用Rocket Fx应用来计算稳定性。

在《坎巴拉太空计划》中，Rocket Fx计算的该火箭稳定性为1.67，而游戏本身计算的数值同样是1.67，结果完全一致。 宇宙基本原理 《坎巴拉太空计划》拥有8个用于分析宇宙物理的传感器。其中5个用于环境分析，2个用于材料分析，1个用于大气分析。通过这些传感器中的PresMat气压计测量得出，在100米高度的大气压力为100.13千帕。根据《坎巴拉太空计划》维基的信息，100米高度的该数值应为101.324千帕，这种差异符合真实的物理定律。由此，计算得出的露天空气压力为1.225千克/立方米。我在坠落计算中使用了这个数值，结果是正确的。这在理论和实验中都得到了证实。

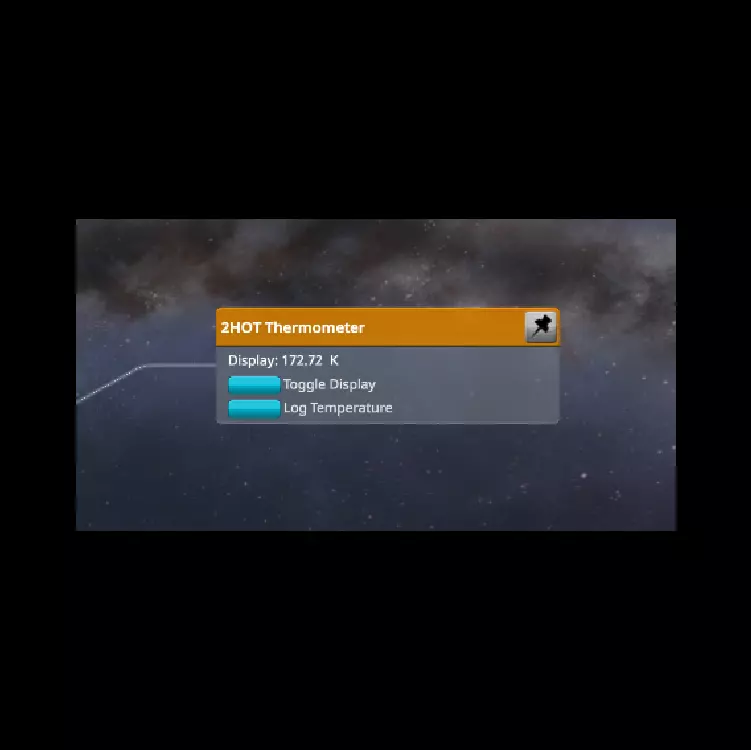
当我们使用2HOT温度计测量太空温度时，得到的数值为172.7K。而实际太空温度应为2.7K。这里可能存在测量或标注上的小数误差。这是我观察到的唯一真实非物理数值。 结论解读 最终结果 总结而言，对于《坎巴拉太空计划》中行星和小行星的运动学与动力学，该游戏是根据真实物理定律建模的。尽管结果不必与地球上的完全相同，但使用相同的公式可以得出相同的实验结果。通过这种方式，人们实际想要进行的太空实验可以通过《坎巴拉太空计划》进行模拟，该游戏或许能为复杂实验创造附加价值。总的来说，这次分析非常成功。无论是对于《坎巴拉太空计划》，还是在《坎巴拉太空计划》维基上发布的慈善性质的Δv地图而言。 Δv计算中的误差值对于一款游戏来说影响不大，因为在飞行过程中可以忽略这个值以到达目的地。根据Δv地图建造的火箭所得到的轨道和计算结果，由于这些计算在现实世界中并不精确，存在一定的范围，而本次分析所计算的是这些区间的平均值。在推重比的计算中，1.67是火箭平稳上升的适中值。对于从地球发射的火箭，推重比通常保持在1.5到2.0之间。这些中间值还表明，火箭不会偏离上升方向太多，足以改变目标。 给想登上空间站的 Kerbonauts 的科学解决方案指南