资深玩家指南，将教你掌握游戏各方面的概率：药水掉落几率、稀有卡牌、强化卡牌、宝箱等。 现在概率站在我们这边 我将告诉你如何不再受随机机制的折磨，并学会预测概率。本指南面向已掌握所有游戏机制且至少达到16级进阶的玩家。在较低的晋升等级时，你可以不用太担心随机性，因为商店里的价格没那么高，事件没那么残酷， bosses 掉落的钱更多，而且强化卡牌出现得更频繁。 如果你是新手，建议跳过机制说明，直接进入“如何将知识应用到实践中”部分。宝箱内容概率 除了仅在第一幕和第二幕末尾出现的首领宝箱外，地图上还可以找到3种类型的宝箱：

小型宝箱，50%生成概率 中型宝箱，33%生成概率 大型宝箱，17%生成概率 它们的区别在于内含遗物的稀有度和金币数量。为什么这很重要？如果宝箱里的东西都会被拿走，那宝箱里有什么不都一样吗？

这一点很重要，因为如果你拥有【诅咒钥匙】遗物，它会在你打开宝箱（除了 boss 宝箱）时给你施加诅咒，所以你不会想打开每一个宝箱。不同类型宝箱中特定稀有度遗物及金币的获取概率 小型 中型 大型 普通遗物 75% 35% 0% 稀有遗物 25% 50% 75% 史诗遗物 0% 15% 25% 金币（概率，数量） 50%（23-27） 35%（45-55） 50%（68-82） 根据上述表格可计算出宝箱平均获得金币数量为18.4枚金币。有50%的概率是小宝箱，其中有1/2的概率平均获得25金币，否则为0金币。 有33%的概率是中宝箱，其中有35%的概率平均获得50金币，否则为0金币。 有17%的概率是大宝箱，其中有1/2的概率平均获得75金币，否则为0金币。 （25×25+25×0+33×0.35×50+33×0.65×0+8.5×75+8.5×0）/100=18.4 【强化卡牌掉落概率】 每通过一个关卡，奖励中强化卡牌的掉落概率都会提升。只有普通和稀有卡牌可以在奖励中获得强化版本。稀有卡牌在不使用特殊遗物的情况下，无法在奖励中获得强化版本。 强化卡牌的掉落概率：第一幕 - 0%，第二幕 - 25%，第三幕 - 50%。从12级升华开始，强化卡牌的掉落概率减半。 稀有卡牌的掉落概率：在与普通敌人、精英敌人战斗后，以及在商人商店中，都可以获得不同稀有度的卡牌。卡牌的掉落稀有度会根据具体情况以及此前多久未掉落稀有卡牌而变化。 战斗 精英 商人 普通 65% 50% 54% 不普通 37% 40% 37% 稀有 3% 10% 9% 稀有卡牌的掉落概率会受到一个修正值的影响，该修正值初始为-5%，每掉落一张普通卡牌，修正值就会增加1%。如果稀有卡牌的概率在应用修正后为负数，那么该概率模块将从普通卡牌的初始概率中扣除（例如，在第一场战斗中，修正后的稀有卡牌概率为-2%，此时我们从普通卡牌的37%概率中扣除该模块，得到35%的普通卡牌概率）。如果稀有卡牌的概率在应用修正值后不为负数，则该修正值不再影响稀有卡牌的概率，且稀有卡牌的实际概率值与初始值（减2）的差值将从普通卡牌的概率中扣除。 当奖励中出现稀有卡牌时，修正值将重置为-5%。然而，商人处和图书馆的卡牌掉落不会影响【卡牌稀有度修正值】，而商人处和图书馆的卡牌稀有度仍然取决于该修正值。击败 Boss 后获得的奖励总是只会掉落稀有卡牌，这会重置【卡牌稀有度修正值】。这意味着在每个章节（除第四章外）第一场战斗的奖励中不会出现稀有卡牌。获得至少1张稀有卡牌的概率 根据上述信息，我们可以计算在不同战斗序列中获得至少1张稀有卡牌的概率。我们将单独计算包含以下情况的战斗序列的平均概率：从第6层开始的随机楼层中战胜1次精英怪（此前不会刷新精英怪），以及战胜2次精英怪。每个幕的概率相同。此外，我们还将计算拥有4个圣物时的概率，这些圣物会显著调整获得至少一张稀有卡牌的几率。

祈祷鼓（击败普通敌人后可获得额外奖励卡牌）。调整值很容易计算，只需将下表中的战斗次数乘以2即可。

名为【问题卡】的遗物（获得奖励时可增加可用卡牌数量1）。表格中分别列出了【破碎皇冠】单独存在时（玩家可选择4张卡牌）和与其共存时（可选择2张卡牌）的数值。

破碎王冠（减少获得奖励时的可用卡牌数量2张）。表格中显示战斗后仅掉落1张卡牌的概率。真是令人沮丧的景象。

Дар Н'лота (утраивает вероятность нахождения редких карт в награду за убийство врагов). Реликвия действует неочевидным образом. Вместо того, чтобы утраивать шанс выпадения редкой карты после применения модификатора, реликвия утраивает базовый шанс выпадения редкой карты (0.03 * 3) и только затем к этому значению применяется модификатор. Это приводит к тому, что эффективность Дара Н'Лота обратно пропорциональна числу выпавших обычных карт считая с последней полученной редкой карты. Из-за чего она теоретически позволяет в каждой награде получать редкую карту (минимальный шанс становится 0.03 * 3 - 0.05 = 0.04 или же 4%), но уже при 10 выпавших обычных картах увеличивает шанс дропа редкой карты всего лишь в 1.75 раза по сравнению с дропом при том же числе выпавших обычных карт без неё (0.03 * 3 + 0.05 = 0.14 или же 14% против 0.03 + 0.05 = 0.8 или же 8%)Дроп хотя бы одной редкой карты, % битвы базовый шанс 1 элита 2 элиты Карта ? Карта ? и Разб. Кор. Разб. Кор. Дар Н'лота 1 0 0 0 0 0 0 4 2 9,87 9,87 9,87 12,9 6,71 3,42 26,01 3 18,54 18,54 18,54 23,66 12,9 6,71 41,76 4 26,24 26,24 26,24 32,97 18,54 9,87 54,9 5 32,97 32,97 32,97 40,96 23,66 12,9 65,66 6 38,86 39,48 39,98 47,76 28,34 15,81 74,32 7 44,04 44,99 45,9 53,5 32,62 18,54 81,16 8 48,62 49,84 50,98 58,36 36,54 21,14 86,49 9 52,68 54,13 55,38 62,51 40,13 23,6 90,56 10 56,31 57,92 59,2 66,07 43,43 25,92 93,62 11 59,55 61,28 62,55 69,12 46,47 28,12 95,85 12 62,47 64,28 65,5 71,76 49,26 30,20 97,43 13 65,10 66,96 68,10 74,05 51,83 32,17 98,5 Шансы высчитаны с помощью deepseek. https://chat.deepseek.com/share/oj3pbfjchbesl6qyv8 Шансы на дроп зелья Зелья могут выпадать в качестве награды после боя. Если игра решила выдать вам зелье, то такими будут шансы на получение зелья определённой редкости: Обычное зелье – 65% Необычное зелье – 25% Редкое зелье – 10% Вероятность выпадения зелья по умолчанию составляет 40% и сбрасывается в начале каждого акта. При дропе зелья шанс получить следующее падает на 10%. Если же среди наград не было зелья, то шанс на дроп растёт на 10%. Таким образом мы можем вывести вероятность нахождения хотя бы одного зелья за череду последовательных боёв в начале акта. Проведя более комплексные вычисления, можно найти вероятность дропа как минимум двух зелий за череду последовательных боёв в начале акта. Сами вычисления оставлю в конце руководства. Таблица вероятностей дропа как минимум одного и как минимум двух зелий за череду битв, % битвы min 1 min 2 1 40 - 2 70 12 3 88 35,2 4 96,4 61,6 5 99,1 79 6 99,928 90,76 Важное уточнение: после использования дымовой шашки или после завершения события «Колизей» игра может попытаться дать зелье в качестве награды, но в случае успеха зелье всё равно не будет отображено, однако это также скажется на шансе получить следующее зелье в большую или меньшую сторону. Реликвии Котёл и Маленький домик выдают зелья совершенно случайно, игнорируя степень редкости.

金钱机会

玩家在普通战斗中获胜可获得10-20枚金币。击败精英敌人可获得25-35枚金币。而击败 Boss 可获得95-105枚金币（【等级13】时为71-79枚）。 前往商人处的途中，玩家可以通过计算商人前的普通战斗和精英战斗次数，并按每场战斗的平均收益（分别为15枚和30枚金币）来预估自己能用于采购的金币总额。了解“商人商品”栏目中的信息后，还能大致了解已攒的钱够买些什么。 商人商品 “独自行动很危险！把你的金子交给我！”【商人】 商人处遗物和药水的出现概率取决于其稀有度： - 遗物：普通50%、稀有33%、罕见17% - 药水：普通65%、稀有25%、罕见10% 随机对一张彩色卡牌应用50%折扣。商人处必定有一个专属遗物，其稀有度等同于普通。从16级开始，所有商品价格上涨10%。商品价格取决于稀有度（括号内为向下取整的平均值） 【普通】 - 地图：45-55（50） - 无色彩地图：- - 圣物：143-158（150） - 药水：48-53（50） 【稀有】 - 地图：135-165（150） - 无色彩地图：162-198（180） - 圣物：285-315（300） - 药水：95-105（100） 此价格表适用于等级16及以上 【普通】 - 地图：50-61（55） - 无色彩地图：- - 圣物：157-173（165） - 药水：52-58（55） 【稀有】 - 地图：149-182（165） - 无色彩地图：178-218（198） - 圣物：314-347（330） - 药水：105-116（110）

如何将这些知识应用到实践中？ 在第一幕初期，一个不错的主意是优先选择战斗而非隐藏房间，这样可以为初始的单薄牌组添加一张免费的稀有卡牌。 如果你打算去拜访商人并想从他那里购买稀有卡牌，那么选择战斗和/或精英怪数量最多的路线。这样你就能“叠加”稀有卡牌的掉落加成，从而提高在商人处找到稀有卡牌的几率，并且这些卡牌不会重置该加成。不过要注意，如果在商人前的奖励中获得了稀有卡牌，那么加成将会重置为-5%。

这里要单独提一下【星盘圣物】，它能让你5次选择卡牌作为奖励，但此时稀有卡牌的出现概率将与出售该圣物的商人相同。所以如果看到商人出售稀有卡牌，不妨考虑购买【星盘圣物】。

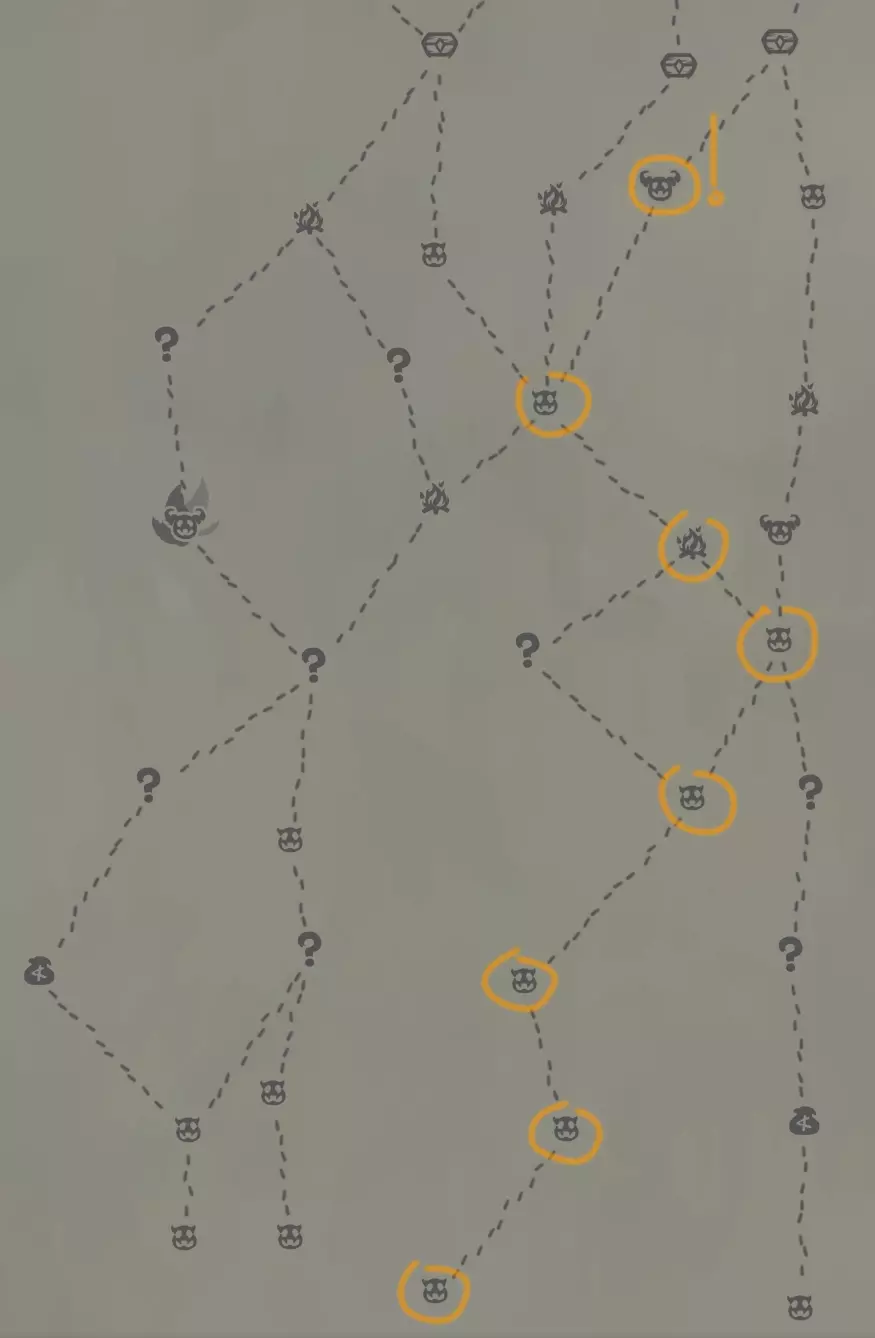
Когда в начале игры вы составляете карту маршрута, то можете нацелиться на элитного врага, путь к которому пролегает через 5-6 обычных битв, чтобы быть уверенным, что в бою у вас будет как минимум 1 или 2 зелья. В примере на картинке вы можете увидеть ситуацию, в которой игрок может быть уверен на 99,928%, что у него будет как минимум 1 зелье в бою с элитой и на 90,76%, что к тому моменту получит как минимум 2 зелья. Перед встречей с этой элитой с шансом 38,86% игрок сможет бесплатно получить редкую карту. За 6 обычных битв и одну побеждённую элиту игрок заработает в среднем 120 золота. А уже после победы над Элитой игрок найдёт Сундук. В среднем из каждого сундука игрок получает 18,4 золота. Если в следующей локации игрока будет ожидать торговец, то к этому моменту в карманах будет в среднем 237,4 золотых монет (учитывая 99 стартовых). Этого точно хватит на реликвию обычной редкости (но не выше) или редкую карту и на сдачу останется купить обычное зелье/обычную карту/необычную карту по скидке/услугу по удалению карты. Если дальше на пути находится ещё один элитный враг, это точно будет другой элитный враг, не тот, которого игрок одолел последним. Шансы на дроп двух зелий за несколько боёв Расчёты для вероятности найти как минимум 2 зелья за 3 боя. Сначала найдём все удачные исходы. Буквой У отмечу бои, в которых игрок получил зелье и буквой Н те, в которых зелье не дропнулось. Затем для каждого такого исхода посчитаем вероятности, а после сложим. Это и будет шанс получить как минимум 2 зелья за 3 боя. исходы У - У - У и У - У - Н мы можем посчитать как У - У, поскольку уже после второго боя в этих исходах зелье есть. 0.4 * 0.3 = 0.12 (12%) при высчитывании Н берём обратный шанс от У У - Н - У 0.4 * 0.7 * 0.4 = 0.112 (11,2%) Н - У - У 0.6 * 0.5 * 0.4 = 0.12 (12%) 12% + 11,2% + 12% = 35,2%. Таким будет шанс нахождения хотя бы двух зелий за 3 боя Теперь посчитаем вероятность нахождения хотя бы двух зелий за 4 боя. Мы будем использовать уже готовые расчёты, если два зелья выпадут за первые 3 боя (35,2%) и добавим к ним те шансы, когда второе зелье выпадает в четвёртом бою. У - Н - Н - У 0.4 * 0.7 * 0.6 * 0.5 = 0.084 (8,4%) Н - У - Н - У 0.6 * 0.5 * 0.6 * 0.5 = 0.09 (9%) Н - Н - У - У 0.6 * 0.5 * 0.6 * 0.5 = 0.09 (9%) 35,2% + 8,4% + 9% + 9% = 61,6%. Таким будет шанс нахождения хотя бы двух зелий за 4 боя. Теперь посчитаем вероятность нахождения хотя бы двух зелий за 5 боёв. Мы будем использовать уже готовые расчёты, если два зелья выпадут за первые 4 боя (61,6%) и добавим к ним те шансы, когда второе зелье выпадает в пятом бою. У - Н - Н - Н - У 0.4 * 0.7 * 0.6 * 0.5 * 0.4 = 0.0336 (3,36%) Н - У - Н - Н - У 0.6 * 0.5 * 0.6 * 0.5 * 0.4 = 0.036 (3,6%) Н - Н - У - Н - У 0.6 * 0.5 * 0.6 * 0.5 * 0.6 = 0.054 (5,4%) Н - Н - Н - У - У 0.6 * 0.5 * 0.4 * 0.7 * 0.6 = 0.0504 (5,04%) 61,6% + 3,36% + 3,6% + 5,4% + 5,04% = 79%. Таким будет шанс нахождения хотя бы двух зелий за 5 боёв. Теперь посчитаем вероятность нахождения хотя бы двух зелий за 6 боёв. Мы будем использовать уже готовые расчёты, если два зелья выпадут за первые 5 боёв (79%) и добавим к ним те шансы, когда второе зелье выпадает в шестом бою. У - Н - Н - Н - Н - У 0.4 * 0.7 * 0.6 * 0.5 * 0.4 * 0.7 = 0.02352 (2,352%) Н - У - Н - Н - Н - У 0.6 * 0.5 * 0.6 * 0.5 * 0.4 * 0.7 = 0.0252 (2,52%) Н - Н - У - Н - Н - У 0.6 * 0.5 * 0.6 * 0.5 * 0.4 * 0.7 = 0.0252 (2,52%) Н - Н - Н - У - Н - У 0.6 * 0.5 * 0.4 * 0.7 * 0.4 * 0.7 = 0.02352 (2,352%) Н - Н - Н - Н - У - У 0.6 * 0.5 * 0.4 * 0.3 * 0.8 * 0.7 = 0.02016 (2,016%) 61,6% + 2,352% + 2,52% + 2,52% + 2,352% + 2,016% = 90.76%. Таким будет шанс нахождения хотя бы двух зелий за 6 боёв.